Within a few hours of CloudFlare launching its Heartbleed Challenge the truth was out. Not only did Heartbleed leak private session information (such as cookies and other data that SSL should have been protecting), but the crown jewels of an HTTPS web server were also vulnerable: the private SSL keys were accessible through Heartbleed messages.

When we launched the challenge we were unsure if private keys could be accessed, but had started the process of revoking and recreating all the SSL private keys that we manage. When the challenge was defeated in a matter of hours it became obvious that it was fairly easy to find the prime numbers that are at the heart of an RSA private key.
Most of the people who obtained the private SSL key of the challenge server did so by searching the results returned in Heartbleed messages for prime numbers. Testing for prime numbers itself is pretty simple (although slow): find a number and see if it has any divisors. Since the length of the prime numbers (in bits) was known it was just a matter of finding all blocks of 1,024 bits and seeing if they were actually a prime.
Finding one prime is enough to break the private SSL key.
The question we wanted to answer was: "Why was it apparently so easy to find prime numbers in Heartbleed results?" To get to the answer I instrumented a vulnerable version of OpenSSL (1.0.1f) and began the search for the primes and where they end up in memory. Strangely, it seemed that OpenSSL was set up to cleanse memory of primes (and other sensitive values) when they were no longer being used. So, what was going on?
But first a detour into the RSA algorithm and how it is implemented efficiently.
RSA and the Montgomery Reduction
The full details of the RSA cryptographic scheme can be read here, but, the short version is that two large prime numbers (almost always called p and q) are chosen and kept secret. The product of those two numbers is referred to as the modulus, typically called N (N = p x q).
It's safe to make N public (it is part of what's called the public key) because it is believed (by mathematicians and computer scientists) that working out p and q from N is difficult (i.e. it is believed that factoring N is hard as long as p and q are very large).
So, when a brower connects to a site that's using SSL it obtains the public key from the site and the site keeps p and q secret. But the site needs p and q to encrypt data and so they are typically (but not always) held in memory of the server handling the web site.
In the Heartbleed attack is was possible to find one of p or q in the Heartbleed packets that were returned containing blocks of memory from the vulnerable server. Since N is public, once you have either of p or q the other can easily be worked out by dividing N by the prime you've found.
Note, that in one Heartbleed attack a researcher used Coppersmith's Attack. That attack is a complex mathematical attack which means that it's possible to split N into p and q if you find just part of a prime number. Read the details of that here.
In practice, the mathematics used in RSA is rather slow and various schemes have been invented to speed it up. One, which is used by OpenSSL, is known as the Montgomery Reduction.
Deep inside RSA the fundamental operation that has to be performed is a multiplication modulo N. If you are not familiar with the term "modulo N", it simply means "divide by N and take the remainder". For example, here's 13 x 29 modulo 11 (which will be 13 x 29 divided by 11 and take the remainder):
13 x 29 modulo 11 = 377 modulo 11 = 3 (377/11 = 34 remainder 3)
This is a very expensive operation for a computer to perform (and in RSA it is performed repeatedly) because it involves multiplication and division (if you remember long division from school you'll remember how laborious it is: computers find it similarly difficult when compared to addition or subtraction).
In 1985, mathematician Peter Montgomery showed that it was possible to perform 'multiplication modulo N' very quickly as follows. At each step the following is performed:
- A digit from the left number is multiplied by the right number and added to a temporary variable (usually called an accumulator);
- The accumulator is divided by 10 and the decimals are discarded;
- If there are digits remaining in the left number then add to the accumulator the number r where r x 11 plus whatever is currently in the accumulator would be divisible by 10.
- Move on to the next digit if there is one
Accumulator 0 87 Added 3 x 29 8 Divided by 10 10 Added 2 because 2 x 11 + 8 = 30 (divisible by 10) 39 Added 1 x 29 3 Divided by 10
The answer, 3, is in the accumulator. What's important here is that only 'easy' calculations were performed: small multiplications by a single digit and division by 10. In the computer implementation all of this is done in binary with division by 2 instead of 10. Division by 2 is very, very easy to implement on a computer.
Under the hood of OpenSSL
To understand how primes are used inside OpenSSL I instrumented the code to output information about all the memory allocated by OpenSSL and to highlight blocks of memory used for prime numbers. I then processed this information using a small program to produce a picture of memory.
Here's the state of the memory used by OpenSSL when running inside NGINX 1.5.13 just after it has started up. Green blocks are memory in use, black areas are unused and the two red bars are the two primes number p and q that form part of the RSA key.
Each row of the picture is 1,024 bytes. The picture shows a total of about 280KB of memory in use. The primes are being stored in a single location (delving into the source of OpenSSL this is the location of the primes when loaded in the function ssl_set_pkey in ssl_rsa.c).
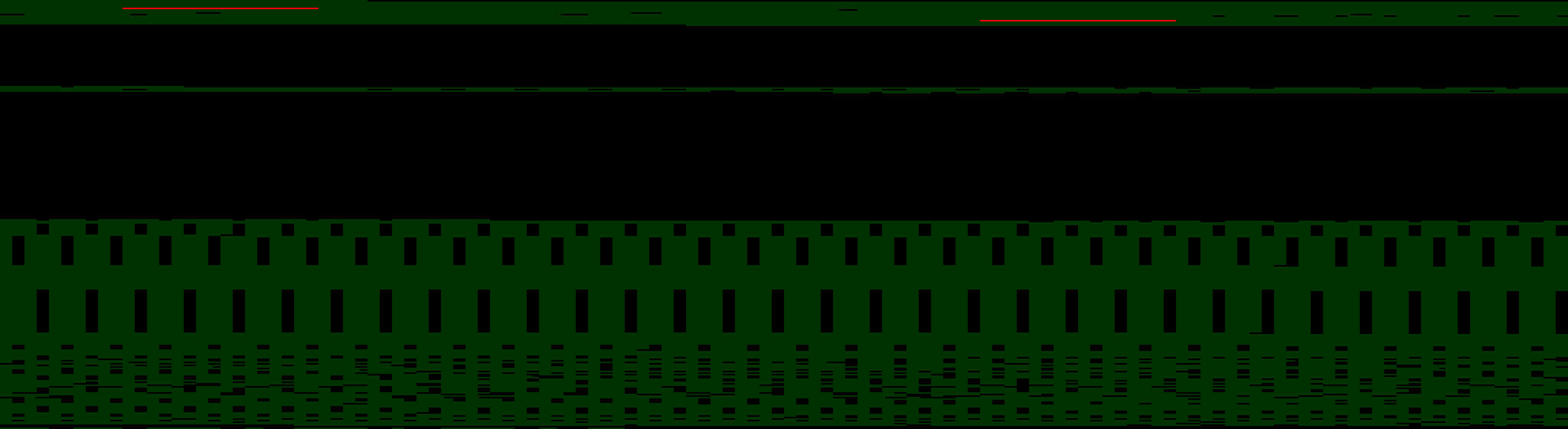
In contrast, something interesting has happen when NGINX/OpenSSL processes its first request. A second copy of the primes has appeared. OpenSSL is now using more memory and two long red lines (two complete primes) are in memory along with some fragments of prime numbers that have been partially overwritten (those are vulnerable to Coppersmith's Attack).

Delving into the code once more it becomes apparent that the two new primes are copies of p and q made for the Montgomery reduction code in bn_mont.c. The fragments of primes are left over from where p and q were used in calculations.
After ten identical requests the memory layout has changed a little more. The fragments of primes have been overwritten, but the Montgomery reduction copies are still there. And some new fragments have appeared.
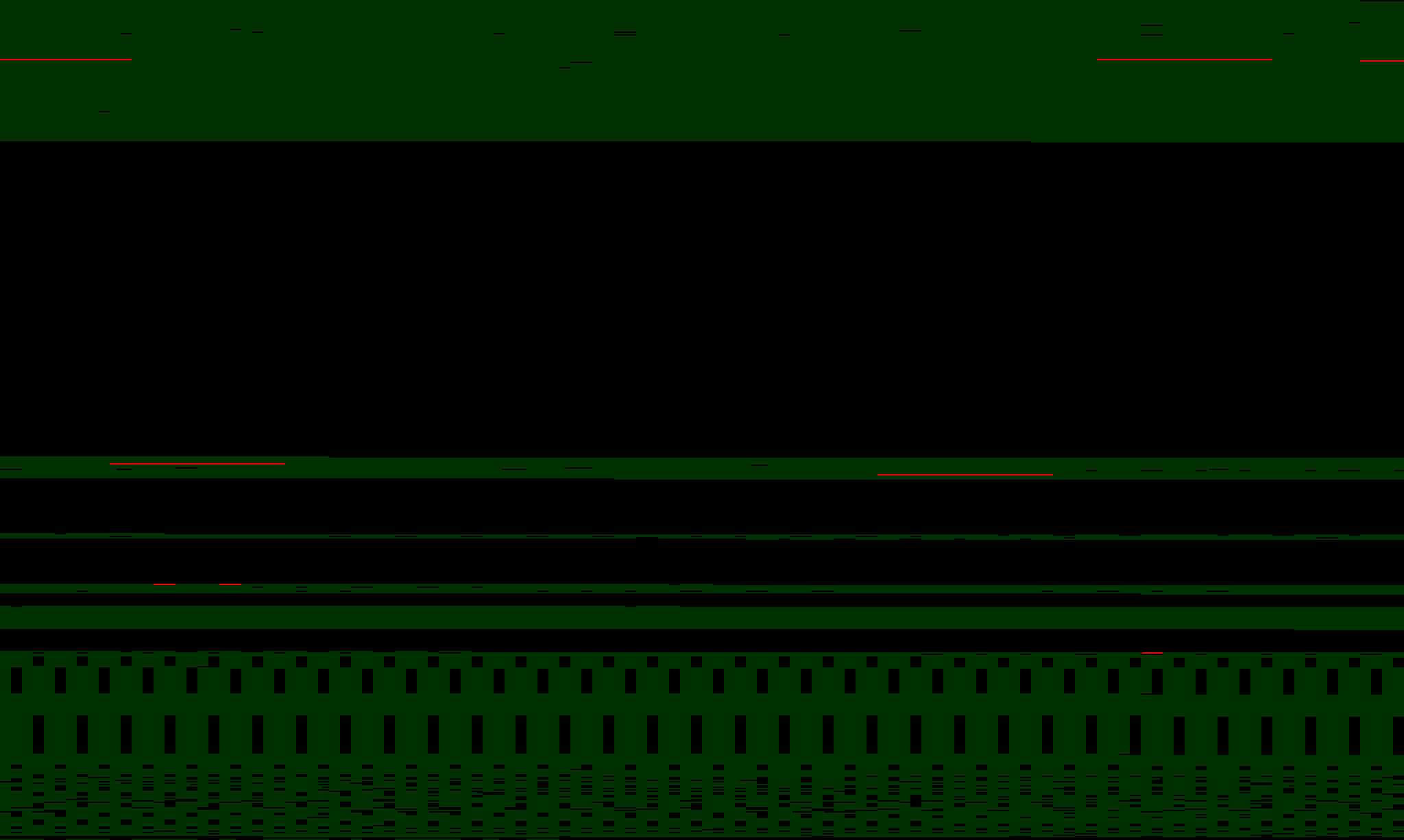
After running a more realistic simulated load through the web server the memory has grown and most of the prime fragments have been overwritten leaving the original primes and the Montgomery reduction primes in memory.

To get a sense of how OpenSSL copies the primes around, here's a slightly different visualization. It shows all the memory that stored primes in red (whether or not it was later overwritten). As you can see OpenSSL is making copies of the primes all over its memory space.
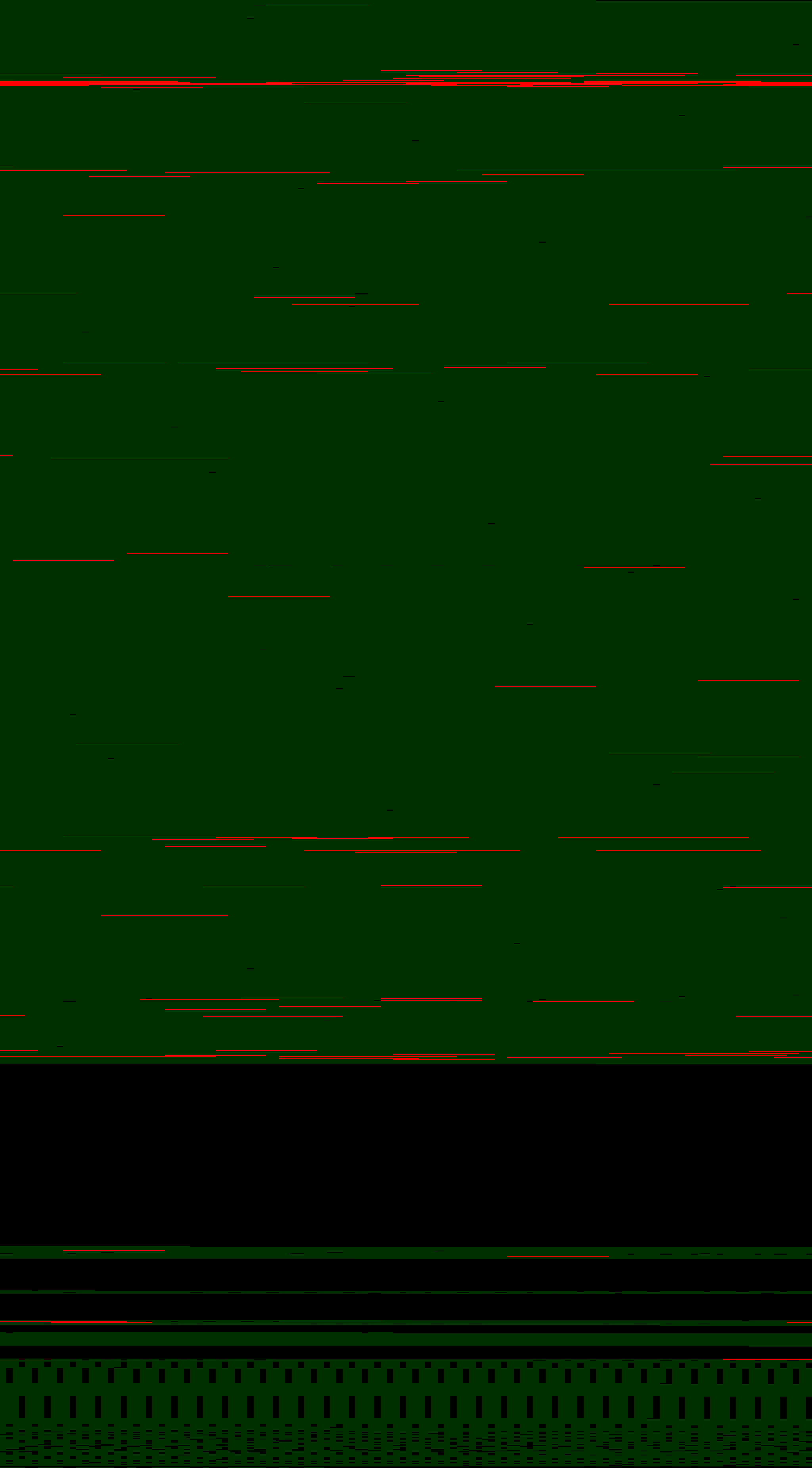
And therein lies the heart of Heartbleed: there are two copies of the primes that never move (the original location where they are loaded and the location of the Montgomery reduction copy) and lots of temporary copies of the primes all over OpenSSL's memory.
OpenSSL patches
It's possible to clean up OpenSSL's memory so that copies of primes are not left in memory by applying the following patch:
diff -ur openssl-1.0.1g/crypto/bn/bn_lib.c openssl-1.0.1g-sanitise/crypto/bn/bn_lib.c
--- openssl-1.0.1g/crypto/bn/bn_lib.c 2014-03-17 09:14:20.000000000 -0700
+++ openssl-1.0.1g-sanitise/crypto/bn/bn_lib.c 2014-04-19 07:57:53.489932751 -0700
@@ -431,7 +431,13 @@
{
BN_ULONG *a = bn_expand_internal(b, words);
if(!a) return NULL;
- if(b->d) OPENSSL_free(b->d);
+
+ if (b->d != NULL)
+ {
+ OPENSSL_cleanse(b->d,b->dmax*sizeof(b->d[0]));
+ OPENSSL_free(b->d);
+ }
+
b->d=a;
b->dmax=words;
}
This patch fixes a problem where the bn_expand2 function in bn_lib.c freed memory potentially containing a prime without erasing it first. The patch adds a call to the OPENSSL_cleanse function that safely erases the number from memory before freeing it. The patch ensures the memory is cleaned up. It was sent to the OpenSSL team on April 19 and independently discovered by Rubin Xu.
This particular function is the cause of primes left in freed memory. Whenever OpenSSL needed to resize a number stored in one of its special BIGNUM structures it would free the now too small BIGNUM without erasing the memory.
That alone is not enough to prevent Heartbleed from getting the primes as there are other copies in memory. In testing, I found that the Montgomery reduction primes were particuarly easy to extract using Heartbleed messages. To prevent them from being created its possible to disable caching of the Montgomery parameters by removing the RSA_FLAG_CACHE_PRIVATE in eng_rsax.c (a similar flag exists in rsa_eay.c.
The Montgomery code also doesn't clean up memory that it frees. The following patch corrects that problem.
diff -ur openssl-1.0.1g/crypto/bn/bn_mont.c openssl-1.0.1g-sanitise/crypto/bn/bn_mont.c
--- openssl-1.0.1g/crypto/bn/bn_mont.c 2014-03-17 09:14:20.000000000 -0700
+++ openssl-1.0.1g-sanitise/crypto/bn/bn_mont.c 2014-04-24 17:57:31.445316346 -0700
@@ -345,9 +345,9 @@
if(mont == NULL)
return;
- BN_free(&(mont->RR));
- BN_free(&(mont->N));
- BN_free(&(mont->Ni));
+ BN_clear_free(&(mont->RR));
+ BN_clear_free(&(mont->N));
+ BN_clear_free(&(mont->Ni));
if (mont->flags & BN_FLG_MALLOCED)
OPENSSL_free(mont);
}
Finally, there's always the possibility that the original location the primes were in might get exposed in a Heartbleed message. To protect against that it would be necessary to change the way OpenSSL memory is allocated so that memory allocated for sensitive data (like private keys) is kept far away from the memory buffers used for messages. A patch for this has been submitted to OpenSSL.
Conclusion
A more radical solution is to not store the private keys inside OpenSSL at all. If the private key is not stored in the same process as OpenSSL it will not be accessible via a fault like Heartbleed.
CloudFlare is already testing that configuration. More on that in another blog post.
PS I am very grateful for Matthew Arcus for corresponding with me about this and checking some of my assertions. It was Matthew who first pointed out that the Montgomery Reduction was another source of leaked primes.

