A few weeks ago we introduced Cryptographic Attestation of Personhood to replace CAPTCHAs with USB security keys, and today we announced additional support for on-device biometric hardware. While doing that work, it occurred to us that hardware attestation, proving identity or other properties of a user with a piece of hardware, could have many wider applications beyond just CAPTCHA alternatives and user authentication via WebAuthn. Really, why should someone have to have an account to prove they exist, when their own trusted device can do so?
Attestation in the WebAuthn standard lets websites know that your security key is authentic. It was designed to have good privacy properties baked into policies that must be followed by device manufacturers. The information your security key sends to websites is indistinguishable from that of myriad other keys. Even so, we wanted to do better. If we’re taking attestation out of authentication, then we need to learn only that your security key is authentic — and we’ve designed a new Zero-Knowledge Proof for the browser to do that.
This is part of our work to improve privacy across the Internet. We’ve yet to put this proof of personhood in production, but you can see a demonstration of the technique in action. We’ve seen it work with YubiKeys among others. Most importantly, we’re open-sourcing the code so everyone can benefit and contribute. Read through below for details, as well as next steps.
Introduction
WebAuthn attestation identifies the manufacturer of your hardware security key to the website that wants the attestation. It was intended for deployment in closed settings like financial institutions and internal services where the website already has a preexisting relationship with you. Since logging in identifies you, the privacy impact was minimal. In contrast, any open website that uses attestation, like we do for proof of personhood, learns the make and model of the key you used.
Make and model information doesn’t seem that sensitive, just like the make and model of your car doesn’t seem that sensitive. There are a lot of 2015 Priuses out there, so knowing you drive one doesn’t help identify you. But when paired with information such as user agent, language preferences, time of day, etc., it can contribute to building up a picture of the user — just as demographic details, height, weight and clothing together with the make and model of a car combine to make it easier to pinpoint a particular car on the highway. Therefore, browsers have a dialogue when a website obtains this attestation, to make sure users understand that the website is learning information that may help identify them. We take privacy seriously at Cloudflare, and want to avoid learning any information that could identify you.
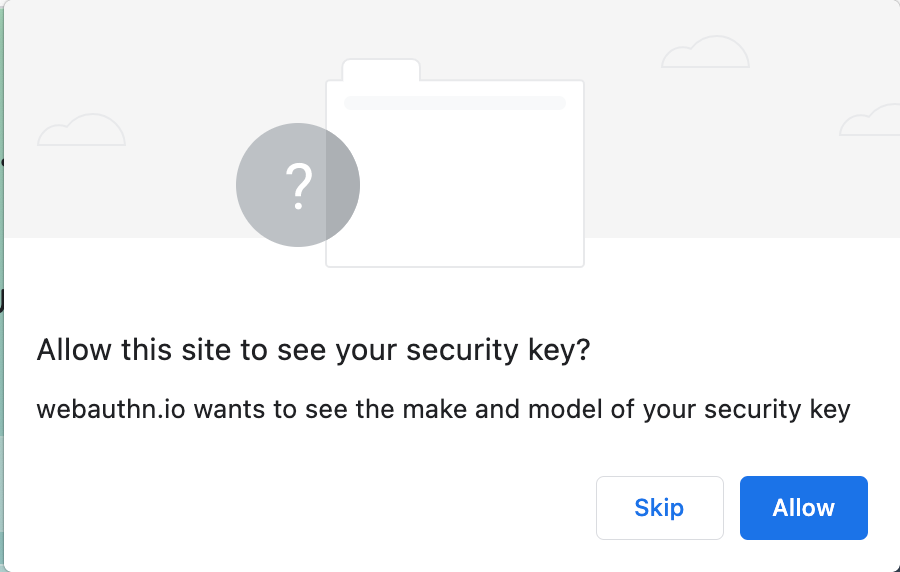
The information that we see from attestation is a proof that the manufacturer of your security key really did make that key. It’s a digital signature using a private key held on your security key in a secure enclave, together with a certificate chain that leads to the manufacturer. These chains enable any server to see that the hardware security key is authentic. All we want for the Cryptographic Attestation of Personhood is a single bit: that you own a hardware security key that is trustworthy, and none of the details about the manufacturer or model.
Historically, attestation has been used in environments where only a few manufacturers were considered acceptable. For example, large financial institutions are understandably conservative. In this environment, revealing the manufacturer is necessary. In an open vendor design, we don’t want to privilege any particular manufacturer, but instead just know that the keys are trustworthy.
Trustworthiness is determined by the FIDO MetaData Service. It is a service from the FIDO2 alliance who maintain root certificates for the manufacturers. When these keys are compromised, they are listed as such in the FIDO system. We have automated scripts to download these roots and insert them into releases of our software. This ensures that we are always up-to-date as new manufacturers emerge or older devices are compromised as attackers extract the keys or the keys get mishandled.
To their credit, the FIDO consortium requires that no fewer than 100,000 devices all share an attestation key, setting a lower bound on the device anonymity set size to minimize the impact of information collection. Alas, this hasn’t always happened. Some manufacturers might not have the volume necessary to ever get that batch size, and users shouldn’t have to flock to the biggest ones to have their privacy protected. At Cloudflare, we have a strong privacy policy that governs how we use this information, but we’d prefer not to know your key’s manufacturer at all. Just as we’ve removed cookies that we no longer needed, and log data customers need to debug their firewall rules without us being able to see it ourselves, we’re always looking for ways to reduce the information that we can see.
At the same time, we need to make sure that the device that’s responding to our request is a genuine security key and not some software emulation run by a bot. While we don’t care which key it is, we’d like to know that it actually is a key that meets our security requirements and hasn’t been compromised. In essence, we’d like to prove the legitimacy of the credential without learning anything else about it. This problem of anonymous credentials isn’t new, and lots of solutions have been proposed and some even deployed.
However, these schemes typically require that the hardware or software that implements the credential attestation was designed with the specific scheme in mind. We can’t go out and convince manufacturers to add features in a few months, let alone replace all the hardware authentication security keys in the world. We have to instead search for solutions that work with existing hardware.
A high-level introduction to Zero-Knowledge Proof
At first glance, it seems that we have an impossible task. How can I demonstrate that I know something without telling you what it is? But sometimes this is possible. If I claim to have the key to a mailbox, you can put a letter inside the mailbox, walk away, and ask me to read the letter. If I claim to know your telephone number, you can ask me to call you. Such a proof is known as a zero-knowledge proof, often abbreviated ZKP.
A classic example of a zero-knowledge proof is showing to someone that you know where Waldo is in Where’s Waldo. While you could point to Waldo on the page, this would tell the person exactly where Waldo is. If however you were to cover up the page with a big piece of paper that has a small hole that only shows Waldo, then the person could only see that Waldo was somewhere on the page, and would be unable to figure out where. They would know that you know where Waldo is, but not know where Waldo is themselves.

Cryptographers have designed numerous zero-knowledge proofs and ways to hook them together. The central piece in hooking them together is a commitment, a cryptographic envelope. A commitment prevents tampering with the value that was placed inside when it was made, and later can be opened to show what was placed in it. We use commitment schemes in real life. A magician might seal a piece of paper in an envelope to assure the audience that he cannot touch or tamper with it, and later have someone open the envelope to reveal his prediction. A silent auction involves people entering sealed envelopes containing bids that are then opened together, making sure that no one can adjust their bid after they see what others have bid.
One very simple cryptographic protocol that makes use of commitments is coin flipping. Suppose Alice and Bob want to flip a coin, but one of them has a few double-headed quarters and the other can flip a coin so it comes up on the side they want every time. The only way to get a fair flip is for both of them to be involved in a way that makes sure if either is honest, the result is a fair flip. But if they simply each flip a coin and trade the results, whoever goes last could pretend they had gotten the result that would make the desired outcome.
Using a commitment scheme solves this problem. Instead of Alice and Bob saying what their results are out loud, they trade commitments to the results. Then they open the commitments. Because they traded the commitments, neither of them can pretend to have gotten a different result based on what they learned, as then they will be detected when they open the commitments.
Commitments are like wires that tie zero-knowledge proofs together, making bigger and more complicated ones from simple ones. By proving that a value in a commitment has two different properties with different zero-knowledge proofs we can prove both properties hold for the value. This lets us link together proofs for statements like “the value in a commitment is a sum of values in two other commitments” and “the value in a commitment appears in a list” into much more complicated and useful statements. Since we know how to prove statements like “this commitment is one if and only if both of these other commitments are one” and “this commitment is one if either of these two commitments is one” we have the building blocks to prove any statement. These generic techniques can produce a zero-knowledge proof for any statement in NP, although it will be quite slow and complicated by default.
Our Zero-Knowledge Proof system for the browser
In Cryptographic Attestation of Personhood the server sends a message to the browser that the hardware security signs, demonstrating its authenticity. Just as a paper signature ensures that the person making it saw it and signed it, a digital signature ensures the identity of the signer. When we use our zero-knowledge proof, instead of sending the signature, the client sends a proof that the signature was generated by a key on a server provided list.
Because we only send the proof to the server, the server learns only that the attestation exists, and not which hardware security key generated it. This guarantees privacy as the identifying information about the security key never leaves the browser. But we need to make sure that proving and verification are efficient enough to carry out at scale, to have a deployable solution.
We investigated many potential schemes, including SNARKS. Unfortunately the code size, toolchain requirements, and proving complexity of a SNARK proved prohibitive. The security of SNARKS relies on more complicated assumptions than the scheme we ultimately went with. Obviously this is an area of active research and the best technology today is not necessarily the best technology of the future.
For the hardware security keys we support, the digital signature in the attestation was produced by the Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA is itself similar to many of the zero-knowledge proofs we use. It starts with the signer computing a point \(R=kG\) on an elliptic curve for a random value \(x\). Then the signer takes the \(x\) coordinate of the point, which is written as \(r\), and their private key, and the hash of the message, and computes a value \(s\). The pair \((r, s)\) is the signature. The verifier uses \(r\) and \(s\) and the public key to recompute \(R\), and then checks that the \(x\) coordinate matches \(r\).
Unfortunately, the verification equation as commonly presented involves some operations that would need to convert values from one form to another. In a zero knowledge proof these operations are complex and expensive, with many steps. We had to sidestep this limitation to make our system work. To transform ECDSA into a scheme we can work with, our prover sends \(R\) instead, and commits to a value \(z\) computed from \(r\) and \(s\) that simplifies the verification equation. Anyone can take an ECDSA signature and turn it into a signature for our tweaked scheme and vice versa without using any secret knowledge, so it is just as secure as ECDSA.
Since the statement we want to prove has two parts — “the message was signed by a key” and “the key is on the list” — it is natural to break up the problem of proving that statement into two pieces. First, the prover demonstrates that the key inside of a commitment signed the message, and then the prover demonstrates the committed key is on a list. The verifier likewise checks these two parts and if both parts work, indicates that the proof is valid.
To prove that the signature verifies under a key, we had to use a proof that one elliptic curve point is a known power of another. This proof is a fairly straightforward zero-knowledge proof, but some steps themselves require zero-knowledge protocols for proving that points were added correctly and arithmetic was done correctly. This proof consumes the bulk of the time in proof generation and verification. Once this proof is verified, the verifier knows that the message was signed by the committed public key.
The next step is for the prover to find where their key is on the list, and then prove that their key is in the list. To do this we use the zero-knowledge proof developed by Groth and Kohlweiss. Their proof first commits to the binary expansion of the place of the commitment in the list. The prover then proves that binary expansion is made out of bits, and supplies some extra information about how they proved it. With the extra info and the proofs, both sides can compute polynomials that evaluate to zero if the commitment is to a value on the list. This code is surprisingly short for such a complex task.
The verifier then checks the Groth-Kohlweiss proof that the committed key is on the list, and then makes sure the message that was signed is what it should be. This is a very efficient proof, even as the list size grows: the work done per list element is a multiplication. If all matches, then we know that the signature was generated by a sufficiently secure security key, and nothing else. If it does not match we know that something is wrong.
Engineering a more efficient curve
We turned statements about ECDSA signatures into statements about points on the P-256 elliptic curve, and then into statements about arithmetic in the field that P-256 is defined over. These statements are easiest to prove if we have a group with a size matching the size of a field, and so we had to find one. This posed an interesting challenge as it’s the reverse of how we normally do things in cryptography. If you’d like to see how we solved it read on, otherwise skip ahead.
Most of the time in elliptic curve cryptography we start with a convenient base field, and search for elliptic curves of prime or nearly prime order with the right properties for our application. This way we can pick primes with properties convenient for computer hardware. When it comes to wanting pairing friendly curves, we typically do computer searches for curves whose parameters are given by polynomials that are known.
But here we wanted a curve with a given number of points, and so we would have to use some fairly advanced number theoretic machinery to determine this curve. Our doing so was a big part in getting our zero-knowledge attestation as efficient as it is.
Elliptic Curves and the Complex Plane
Elliptic curves are particularly nice over the complex numbers. An elliptic curve is isomorphic to a torus. All complex curves are isomorphic to tori over the complex numbers, but some have more than one hole.
Different elliptic curves are distinguished by how fat or thin the two directions around the torus are with respect to one another. If we imagine slicing around the holes in the torus, we see that we can get a torus from taking a rectangle and gluing up the sides. There is an illustrative video of what this looks like Gluing a torus.
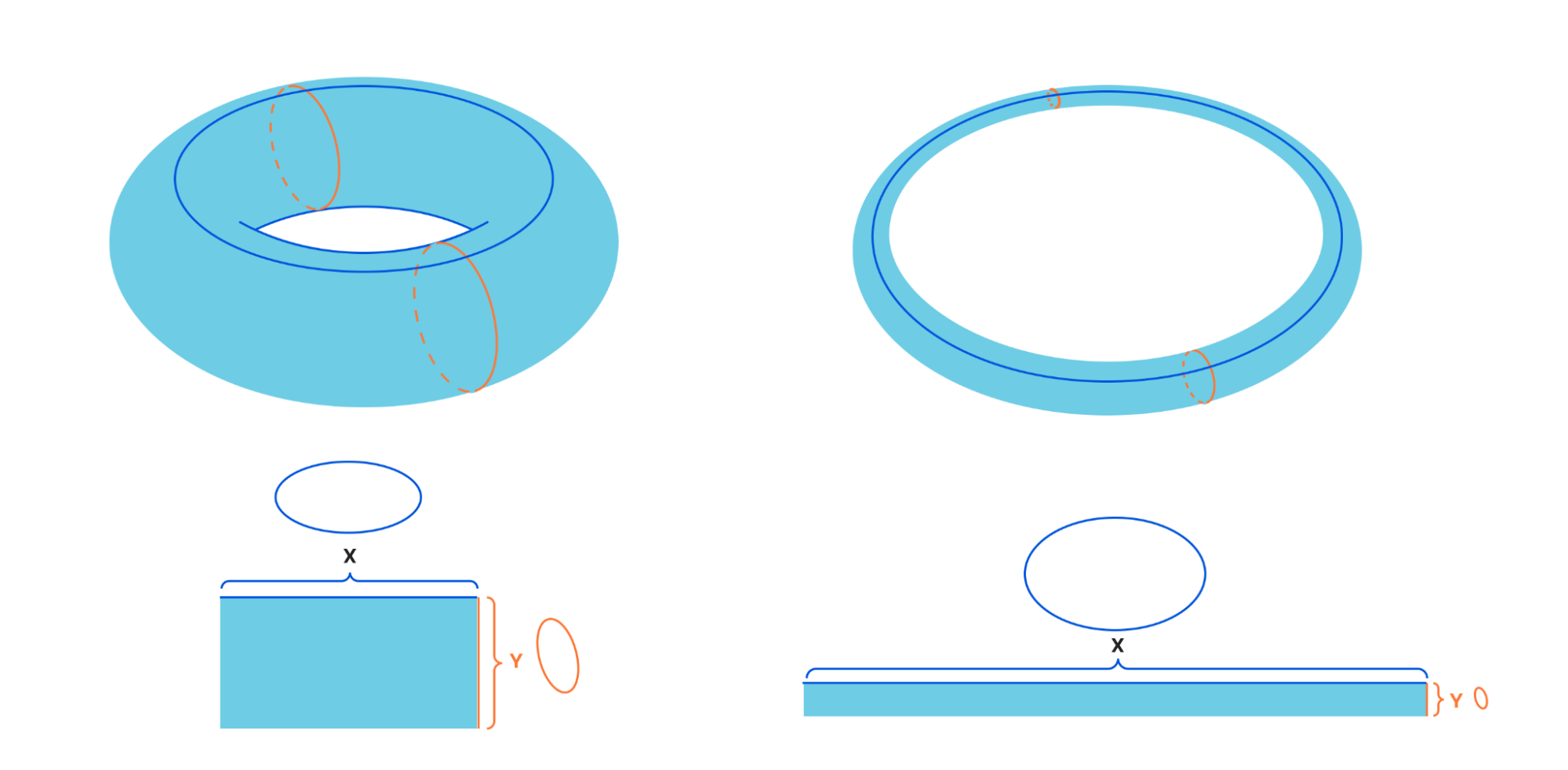
Instead of taking one rectangle and gluing it up, we can imagine taking the entire plane, and then folding it up so that every rectangle lines up. In doing so the corners of these rectangles all line up over the origin. The corners form what we call a lattice, and we can always scale and rotate to have one of the generators of the lattice be 1.
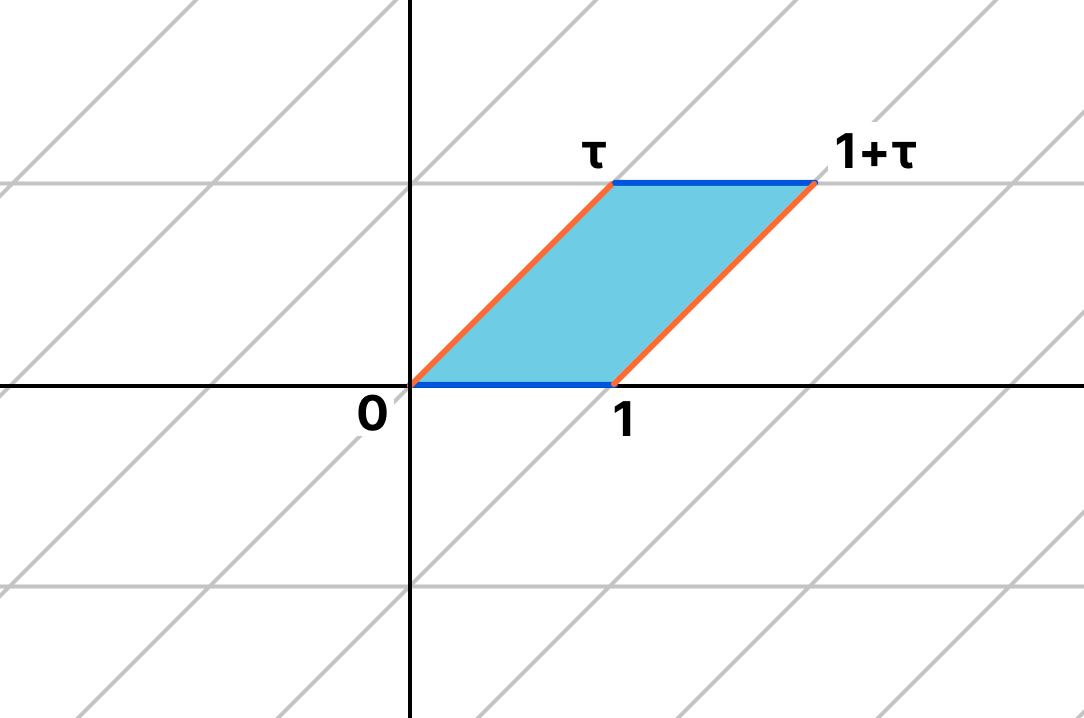
Viewed this way, addition of complex numbers becomes addition on the torus, just as addition of the integers modulo 2 is addition of integers, then reduced mod 2. But with elliptic curves we’re used to having algebraic equations for addition and multiplication, and also for the curves themselves. How does this analytic picture interact with the algebraic one?
Via a great deal of classical complex geometry we find they are closely related. The ring of complex-valued functions on the lattice is generated by the Weierstrass \(\mathcal{P}\) function and its derivative. These satisfy an algebraic equation of the form \(y^2=x^3+ax+b\), and the parameters \(a\) and \(b\) are functions of the lattice parameter. The classical formulas for the algebraic addition of points on elliptic curves emerge from this.
One of the parameters is the \(j\) invariant, which is a more arithmetically meaningful invariant than \(\tau\). The \(j\) invariant is an invariant of the elliptic curve: values of \(\tau\) that give rise to the same lattice produce the same \(j\) invariant, while they may have different \(a\) and \(b\). There are many expressions for \(j\), with one being
https://dlmf.nist.gov/23.15#E7
Complex multiplication and class number
Suppose we take the lattice \(\{1, i\}\). If we multiply this lattice by \(i\), we get back \(\{i, -1\}\), which generates the same set of points. This is exceptional, and can only happen when the number we multiply by satisfies a quadratic equation. The elements of the lattice are then closely related to the solutions of that quadratic equation.
Associated with such a lattice is a discriminant: the discriminant of the quadratic field associated with the example. For our example with i the discriminant is \(-4\), the discriminant of the quadratic equation \(x^2+1\). If, for instance, we were to take \(\sqrt{-5}\) instead and consider the lattice \( \{1, \sqrt{-5}\} \), the discriminant would be \(-20\), the discriminant of \(x^2-5\). Note that there are different definitions of the discriminant, which change the sign and add various powers of \(2\).
Maps from elliptic curves to themselves are called endomorphisms. Most elliptic curves just have multiplication by integers as endomorphisms. But some curves have additional endomorphisms. For instance, if we turn the lattice \(\{1, i\}\) into an elliptic curve, we obtain \(y^2=x^3+x\). Now this curve has an extra endomorphism: if I send \(y\) to \(iy\) and \(x\) to \(-x\), I get a point that satisfies the curve equation as \((-iy)^2=(-x)^3-x\). Doing this map twice produces the same effect as inverting a point, and it’s no coincidence that multiplying twice by \(i\) sends a complex number \(z\) to \(-z\). So this extra endomorphism and multiplying by \(i\) satisfy the same equation. Having an extra endomorphism is called complex multiplication as its multiplication by a complex number. When the lattice an elliptic curve comes from has complex multiplication, the elliptic curve also has complex multiplication and vice versa.
Any set of mathematical objects comes with questions, and elliptic curves with complex multiplication are no exception. We can ask how many elliptic curves with complex multiplication there are for a given discriminant. How does that number grow as the discriminant grows? Some of these questions are still open today, despite years of research and computer experimentation. Key to approaching them is a link between lattices and arithmetic.
Earlier in the 19th century Gauss studied binary quadratic forms, equations of the form \(ax^2+bxy+cy^2\). Such forms are said to be equivalent if there is a substitution with integer coefficients for \(x\) and \(y\) that takes one into the other. This is a core notion, and in addition to algorithms for reducing a binary quadratic form, Gauss demonstrated that there was a composition law that made binary quadratic forms of a given discriminant into a group.
Later number theorists would develop the concept of an ideal, tying quadratic forms to the failure of factorization to be unique. \(x^2+5y^2\)and \(2x^2+2xy+3y^2\) are both quadratic forms of discriminant -20, and this is connected to the failure of unique factorization in \(\mathbb{Z}[\sqrt{-5}]\).
When we consider binary quadratic forms as the lengths of vectors in a plane, each lattice gives a binary quadratic form up to equivalence. The elliptic curves with complex multiplication by a given discriminant thus correspond to the classes of binary quadratic forms with a given discriminant, which connects to the arithmetic in the quadratic field. Three very different looking questions thus all have the same answer.
Why complex multiplication matters for finding curves
When we take an elliptic curve with integral coefficients and consider it over a prime, it gets an extra endomorphism: the Frobenius endomorphism that sends \(x\rightarrow x^p\) and \(ny\rightarrow y^p\) . This endomorphism satisfies a quadratic equation, and the linear term of that quadratic equation is the number of points minus \(p+1\).
If the elliptic curve has complex multiplication, there is another endomorphism, namely the one we get from complex multiplication. But an elliptic curve can only have one extra endomorphism unless it is supersingular. Supersingular curves are very rare. So the Frobenius endomorphism and the endomorphism from complex multiplication must be the same. Because we started out with complex multiplication, we know the quadratic equation the Frobenius must satisfy, and hence the number of points.
This is the conclusion of our saga: to find an elliptic curve with a given order, find integer solutions to the equation \(t^2+Dy^2=4N\) for small \(D\) and let \(p=N-t+1\) and see if it is prime. Then factor the Hilbert class polynomial of \(D\) over \(p\), and take one of the roots modulo \(p\) as the \(j\) invariant of our elliptic curve. We may need to take a quadratic twist to get the right number of points, since t is only identified up to sign.
This gave us the curve we needed for efficient proving of relations over the base field of P-256. All of this mathematics produces a script that runs in a few minutes and produces the curve with the desired order that we needed.
The results of our labor
After all this work, and much additional engineering work needed to make the proof run faster through optimizing little bits of it, we can generate a proof in a few seconds, and verify it in a few hundred milliseconds. This is fast enough to be practical, and means that websites that want to verify the security of security keys can do so without negative privacy impacts.
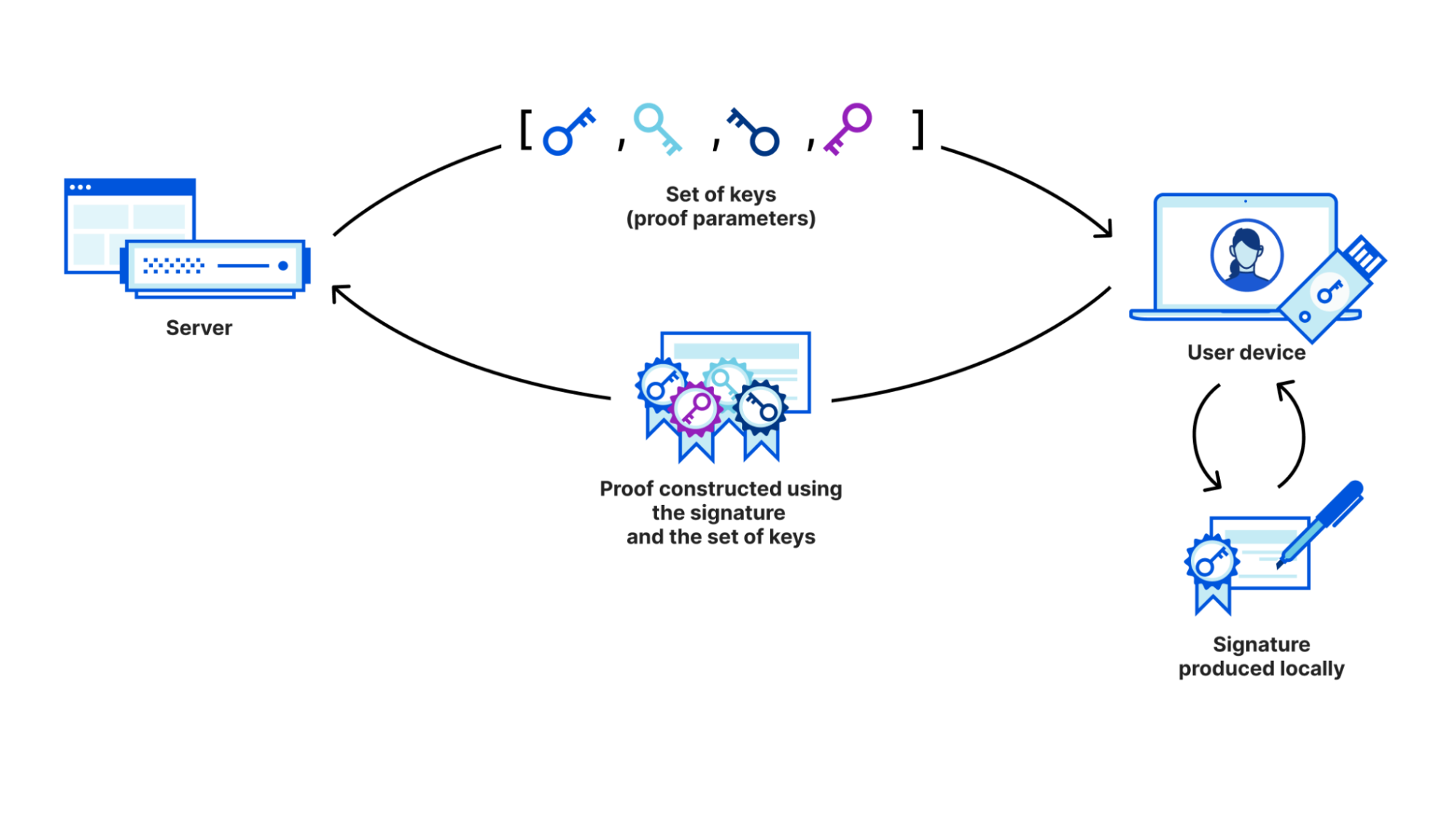
All a website that uses our technique learns is whether or not the signature was generated by a token whose attestation key is on the list they provided. Unlike using WebAuthn directly they do not get any more detailed information, even if the manufacturer has accidentally made the batch too small. Instead of having a policy-based approach to guarding user privacy, we’ve removed the troublesome information.
Next steps — a community effort!
Our demonstration shows that we have a working privacy enhancement based on a zero-knowledge proof. We’re continuing to improve it, adding more performance and security features. But our task isn’t done until we have a privacy-preserving WebAuthn extension that works in every browser, giving users assurance that their data is not leaving the device.
What we have now is a demonstration of what is possible: using zero-knowledge proofs to turn WebAuthn attestation into a system that treats every manufacturer equally by design, protects user privacy, and can be used by every website. The challenges around user privacy that are created by using attestation on a wide scale are solvable.
There’s much more that goes into a high-quality, reliable system than the core cryptographic insights. In order to make the user experience not involve warnings about the information our zero-knowledge proof discards, we need more integration with the browser. We also need a safe way for users of devices not on our list to send their key to us and demonstrate that it should be trusted, and a way to make sure that the list isn’t being abused to try to pinpoint particular keys.
In addition, this verification is more heavyweight than the older verification methods, so servers that implement it need to incorporate rate limiting and other protections against abuse. SNARKS would be a big advantage here, but comes at a cost of code size for the demonstration. Ultimately bringing these improvements into a core part of the web ecosystem requires working with users, browsers, and other participants to find a solution that works for them. We would like to hear from you at [email protected] if you would like to contribute to the process.
Our Cryptographic Attestation of Personhood gives users an easier way to demonstrate their humanity, and one which is more privacy-preserving than many CAPTCHA alternatives or providers. But we weren’t satisfied with the state of the art and saw a way to apply advanced cryptography techniques to improve the privacy of our users. Our work shows zero-knowledge proofs can enhance the privacy offered by real world protocols.

