Il y a quelques semaines, nous présentions le concept d'attestation cryptographique de personnalité pour remplacer les CAPTCHA par des clés de sécurité USB. Aujourd'hui, nous annonçons la prise en charge supplémentaire des équipements biométriques sur l'appareil. Pendant ce travail, nous avons constaté que l'attestation physique (c'est-à-dire le processus permettant de prouver l'identité ou d'autres propriétés d'un utilisateur à l'aide d'un équipement matériel) pourrait avoir beaucoup un champ d'application bien plus large, au-delà de la simple alternative aux CAPTCHA et à l'authentification des utilisateurs via WebAuthn. De fait, pourquoi ces derniers devraient-ils disposer d'un compte pour prouver leur existence alors que leur propre appareil de confiance peut le faire pour eux ?
La procédure d'attestation selon la norme WebAuthn permet aux sites web de vérifier l'authenticité de votre clé de sécurité. Cette norme a été conçue de manière à offrir de solides propriétés en matière de confidentialité, directement intégrées aux politiques que les fabricants d'appareils doivent respecter. Les informations envoyées par votre clé de sécurité aux sites web ne présentent ainsi aucune différence avec celles envoyées par une myriade d'autres clés. Toutefois, nous souhaitions aller plus loin. Si nous supprimons la partie attestation du processus d'authentification, il nous suffit de savoir que votre clé de sécurité est authentique. C'est en partant de ce postulat que nous avons conçu une nouvelle preuve à divulgation nulle de connaissance pour le navigateur.
L'amélioration de la confidentialité sur Internet fait partie de notre travail. Nous devons encore mettre cette preuve de personnalité en production, mais vous pouvez d'ores et déjà voir une démonstration pratique de cette technique. Nous avons ainsi pu constater sa compatibilité avec YubiKeys, entre autres solutions. Plus important encore, nous comptons publier le code en open-source afin que chacun puisse en bénéficier et y contribuer. Vous trouverez les détails à ce sujet et les prochaines étapes à venir ci-dessous, en poursuivant votre lecture.
Introduction
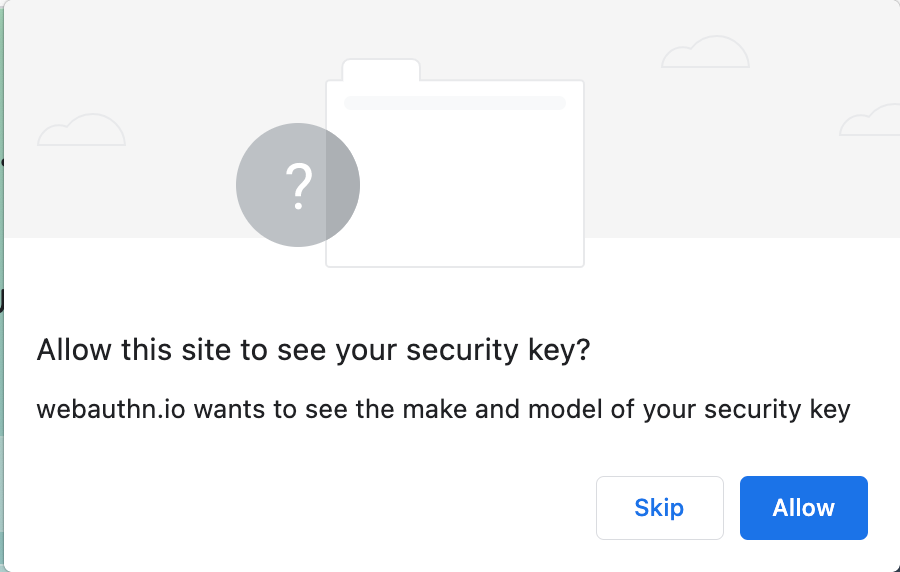
L'attestation WebAuthn identifie le fabricant de votre clé de sécurité physique auprès du site web qui souhaite obtenir cette attestation. Cette procédure était prévue pour un déploiement en environnement fermé, comme les institutions financières et les services internes, au sein desquels une relation préexiste entre le site web et l'utilisateur. Comme le processus même de connexion identifie déjà ce dernier, l'impact sur la vie privée se révèle minime. À l'inverse, tout site web ouvert recourant à la procédure d'attestation (comme nous le faisons avec la preuve de personnalité) apprendra la marque et le modèle de la clé que vous avez utilisée.
Les informations relatives à la marque et au modèle de cette dernière ne paraissent pas revêtir un caractère particulièrement sensible, tout comme la marque et le modèle de votre voiture ne le semblent pas non plus. Le parc automobile mondial recèle un grand nombre de Prius 2015, aussi savoir que vous en conduisez une n'aide pas spécialement à vous identifier. Toutefois, associées à d'autres informations, comme l'agent utilisateur, les préférences linguistiques, l'heure de la journée, etc., elles peuvent contribuer à dresser un portrait de l'utilisateur, sur le même principe que les informations d'ordre démographique ou les données relatives à la taille, au poids et aux vêtements portés peuvent, en association avec la marque et le modèle d'une voiture, permettre de faciliter le repérage d'un véhicule particulier sur l'autoroute. Les navigateurs affichent donc une boîte de dialogue lorsqu'un site web obtient cette attestation, afin de s'assurer que l'utilisateur comprend bien que le site web apprend des informations susceptibles d'aider à l'identifier. Cloudflare prend les questions de confidentialité très au sérieux. Nous souhaitons donc éviter d'avoir connaissance de toute information capable de vous identifier.
Les informations que nous obtenons du processus d'attestation constituent la preuve que le fabricant de votre clé de sécurité a réellement fabriqué cette clé. Elles se présentent sous la forme d'une signature numérique par clé privée placée au sein d'une enclave sécurisée sur votre clé de sécurité et d'une chaîne de certificats remontant jusqu'au fabricant. Ces chaînes permettent à n'importe quel serveur de constater l'authenticité d'une clé de sécurité physique. La seule information que nous souhaitons voir véhiculée par l'attestation cryptographique de personnalité tient au fait que « vous possédez une clé de sécurité physique digne de confiance », sans révéler aucun détail sur le fabricant ou le modèle donc.
Historiquement, la procédure d'attestation n'était employée qu'au sein de certains environnements, dans lesquels seuls quelques fabricants étaient considérés comme acceptables. Les grandes institutions financières, par exemple, font naturellement preuve d'une grande prudence. La révélation du nom du fabricant s'avère donc nécessaire dans ce contexte. Pour une conception à prestataire libre, nous ne souhaitons pas privilégier un fabricant particulier, mais uniquement savoir que les clés se montrent dignes de confiance.
La fiabilité est déterminée par le service de métadonnées FIDO, un service de l'alliance FIDO2 conservant les certificats racine des fabricants. En cas de compromission des clés, ces dernières sont alors répertoriées comme telles dans le système FIDO. Nous disposons de scripts automatisés pour télécharger ces racines et les insérer dans les versions de nos logiciels. Cette opération nous permet de nous assurer que nous restons constamment à jour, même lorsque de nouveaux fabricants apparaissent sur le marché ou que des appareils plus anciens se révèlent compromis, du fait d'un mauvais traitement des clés ou suite à l'extraction des clés par les pirates.
À son crédit, le consortium FIDO nécessite que pas moins de 100 000 appareils partagent la même clé d'attestation, fixant ainsi une limite inférieure à la taille de l'ensemble nécessaire à l'anonymisation des appareils, afin de minimiser l'impact de la collecte d'informations. Un constat qui n'est pas toujours le cas en pratique, car certains fabricants peuvent ne pas travailler avec les volumes nécessaires pour atteindre un jour cette taille de lot. D'ailleurs, les utilisateurs ne devraient pas avoir à se ruer vers les plus gros fournisseurs pour s'assurer du respect de leur confidentialité. Chez Cloudflare dispose d'une solide politique de confidentialité régissant la manière dont nous utilisons ces informations, mais nous préférons ne pas connaître le nom du fabricant de votre clé. Tout comme nous avons supprimé les cookies dont nous n'avions plus besoin et les données de journal dont les clients ont besoin pour déboguer leurs règles de pare-feu sans possibilité de les voir de notre côté, nous sommes toujours à la recherche de moyens permettant de réduire les informations que nous sommes susceptibles de voir.
Nous devons également nous assurer que l'appareil qui répond à notre requête constitue une vraie clé de sécurité et non une émulation logicielle exécutée par un bot. Le modèle de la clé nous importe peu, nous souhaitons simplement nous assurer qu'il s'agit bien d'une clé conforme à nos exigences de sécurité et qu'elle n'a pas été compromise. Concrètement, nous aimerions pouvoir prouver la légitimité des identifiants sans rien apprendre d'autre. Le problème des données d'identification anonymes n'est pas neuf. De nombreuses solutions ont d'ailleurs été proposées à ce titre et certaines ont même été déployées.
Toutefois, la plupart d'entre elles nécessitent généralement que l'équipement physique ou logiciel à l'œuvre derrière l'attestation d'identification soit spécifiquement conçu pour un modèle de solution donné. Nous ne pouvons pas convaincre les fabricants d'ajouter des fonctionnalités en quelques mois et encore moins remplacer l'ensemble des clés physiques chargées de sécuriser les procédures d'authentification à travers le monde. À la place, nous devons chercher des solutions fonctionnant avec le matériel existant.
Présentation générale du concept de preuve à divulgation nulle de connaissance
À première vue, la tâche semble impossible. Comment démontrer que l'on connaît quelque chose sans révéler de quoi il s'agit ? Toutefois, l'opération s'avère parfois possible. Si je prétends détenir la clé d'une boîte aux lettres, vous pouvez glisser une lettre à l'intérieur de cette dernière, vous éloigner et me demander de lire la lettre. Si j'affirme connaître votre numéro de téléphone, vous pouvez me demander de vous appeler. Il s'agit là de ce qu'on nomme une preuve à divulgation nulle de connaissance, souvent abrégée ZKP (pour Zero-Knowledge Proof).
L'énoncé suivant constitue un exemple classique de preuve à divulgation nulle de connaissance : montrer à une personne que vous savez où se trouve Charlie dans les livres Où est Charlie ?. Vous pourriez tout simplement indiquer le personnage du doigt sur la page, mais cette opération révélerait à votre interlocuteur l'endroit exact où se situe Charlie. Toutefois, si vous pouviez couvrir l'intégralité de la page avec une grande feuille de papier dotée d'un petit trou ne découvrant que Charlie, la personne en question pourrait constater que Charlie figure bien quelque part sur la page, mais ne serait pas en mesure de déterminer où. Elle saurait ainsi que vous savez où Charlie se trouve, sans elle-même savoir où ce dernier se situe.

Les cryptographes ont conçu un grand nombre de preuves à divulgation nulle de connaissance et de moyens de les rattacher ensemble. L'élément central permettant de les regrouper repose sur une mise en gage, c'est-à-dire une enveloppe cryptographique. Cette mise en gage prévient l'altération de la valeur placée à l'intérieur de l'enveloppe lors de sa fabrication, tout en permettant à cette dernière d'être ouverte par la suite afin de révéler son contenu. Nous utilisons des schémas de mise en gage dans la vie de tous les jours. Un magicien peut, par exemple, placer un morceau de papier au sein d'une enveloppe scellée de manière à garantir au public qu'il ne peut ni le toucher ni l'altérer d'aucune façon que ce soit, avant de demander ensuite à une personne du public d'ouvrir l'enveloppe, à la fin du numéro, afin de révéler sa prédiction. Une vente aux enchères par écrit implique la saisie d'enchères sur papier de la part des participants à la vente, avant d'enfermer ces propositions au sein d'enveloppes scellées. Ces dernières sont ensuite ouvertes ensemble, afin de s'assurer que personne ne peut ajuster son enchère après avoir vu les montants proposés par les autres.
Un protocole cryptographique très simple qui fait appel aux engagements est le jeu de pile ou face. Imaginons qu'Alice et Bob veuillent jouer à pile ou face, mais que l'un des deux participants dispose de quelques pièces affichant deux piles et que l'autre puisse lancer la pièce de manière à ce que la pièce tombe toujours du côté souhaité. Le seul moyen d'obtenir un tirage équitable serait donc que les deux parties soient impliquées de façon à garantir que si l'un des deux est honnête, le résultat constitue un tirage équitable. Toutefois, s'ils tirent chacun à pile ou face de leur côté avant d'échanger leurs résultats, celui qui procède en dernier peut prétendre avoir obtenu le résultat qui lui permettra d'obtenir le résultat souhaité.
L'utilisation d'un schéma de mise en gage résout ce problème. Plutôt que de laisser Alice et Bob annoncer leurs résultats à voix haute, les deux participants mettent ces résultats en gage, qu'ils s'échangent, avant de les ouvrir de manière simultanée. Comme ils ont échangé leurs gages, aucun d'entre eux ne peut prétendre avoir obtenu un résultat différent sur la base de ce qu'ils ont appris, car ils se feraient alors percer à jour lors de l'ouverture des gages.
Les gages se comportent un peu comme des fils reliant les preuves à divulgation nulle de connaissance entre elles et permettent ainsi de créer des preuves plus élaborées et plus compliquées à partir de preuves simples. En prouvant qu'une valeur mise en gage présente deux propriétés différentes à l'aide de preuves à divulgation nulle de connaissance différentes, nous pouvons prouver que les deux propriétés partagent la même valeur. Ce constat nous permet de relier les preuves étayant les énoncés du type « la valeur d'un élément mis en gage constitue la somme des valeurs de deux autres éléments mis en gage » et « la valeur d'un élément mis en gage apparaît dans une liste » afin de produire des énoncés beaucoup plus complexes et utiles. Puisque nous savons comment prouver les énoncés du type « cet élément mis en gage vaut un, si et seulement si, ces deux autres éléments mis en gage valent un » et « cet élément mis en gage vaut un si l'un de ces deux éléments vaut un », nous disposons des matériaux nécessaires pour prouver n'importe quel énoncé. Ces techniques génériques permettent de produire une preuve à divulgation nulle de connaissance pour n'importe quel énoncé, mais le processus se révélera assez lent et compliqué par défaut.
Notre système de preuve à divulgation nulle de connaissance pour navigateur
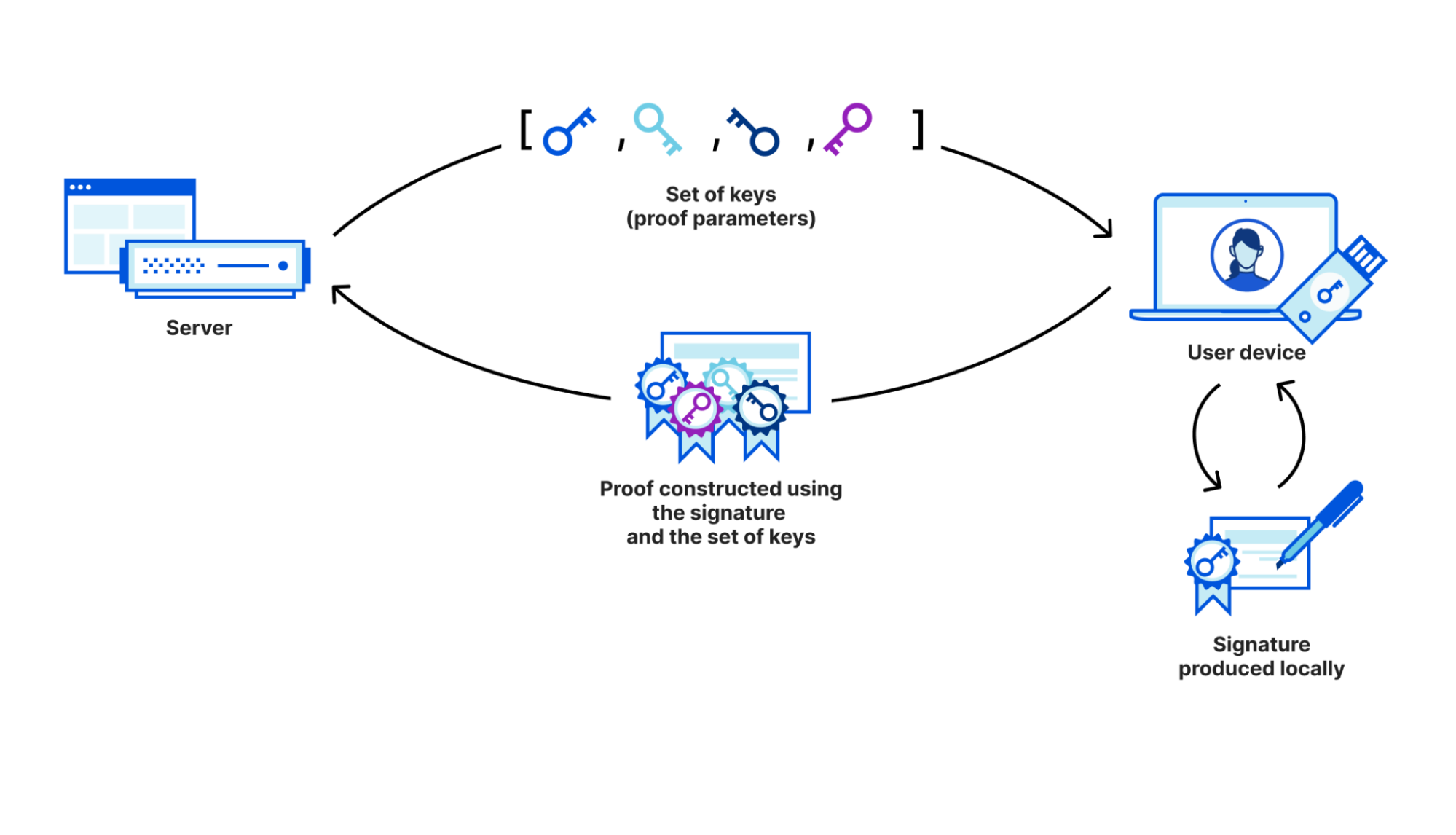
Dans le cas de l'attestation cryptographique de personnalité, le serveur envoie au navigateur un message que l'équipement physique de sécurité signe, afin de démontrer son authenticité. Tout comme une signature sur un document permet de garantir que la personne qui l'appose a bien vu et signé ledit document, la signature numérique garantit l'identité du signataire. Lors de l'utilisation de notre système de preuve à divulgation nulle de connaissance, le client envoie une preuve que la signature a bien été générée par une clé figurant sur une liste fournie par le serveur, plutôt que d'envoyer directement la signature.
Comme nous n'envoyons que cette preuve au serveur, ce dernier apprend uniquement l'existence de l'attestation, sans aucun détail sur la clé de sécurité physique qui l'a générée. Ce procédé garantit donc la confidentialité, car les informations d'identification relatives à la clé de sécurité ne quittent jamais le navigateur. Toutefois, afin de pouvoir disposer d'une solution prête au déploiement, nous devons nous assurer que la preuve et la vérification se montrent suffisamment efficaces dans une situation d'exécution à grande échelle.
Nous avons étudié un grand nombre de schémas potentiels, dont les SNARK (Succinct Non-interactive Argument of Knowledge, argument de connaissance non interactif succinct). Malheureusement, la taille du code, les exigences de la chaîne d'outils et la complexité de la démonstration d'un SNARK se sont avérées prohibitives. La sécurité des SNARK repose sur des hypothèses plus complexes que le schéma que nous avons finalement choisi. En effet, bien qu'il s'agisse d'un domaine de recherche pour le moins actif, la meilleure technologie d'aujourd'hui ne constitue pas nécessairement la meilleure technologie de demain.
Dans le cas des clés de sécurité physiques que nous prenons en charge, la signature numérique de l'attestation a été produite par l'algorithme ECDSA (Elliptic Curve Digital Signature Algorithm, algorithme de signature numérique à courbe elliptique), lui-même similaire à de nombreuses preuves à divulgation nulle de connaissance que nous utilisons. L'opération commence avec le calcul par le signataire d'un point \(R = kG\) situé sur une courbe elliptique pour une valeur aléatoire \(x\). Le signataire prend ensuite la coordonnée \(x\) du point (notée \(r\)), ainsi que sa clé privée et le hachage du message, avant de calculer une valeur \(s\). La paire \((r, s)\) représente la signature. Le vérifieur utilise alors \(r, s\) et la clé publique pour recalculer \(R\), puis vérifie que la coordonnée \(x\) correspond à \(r\).
Malheureusement, l'équation de vérification (telle qu'elle est couramment présentée) implique certaines opérations qui nécessiteraient de convertir des valeurs d'une forme à une autre. Dans une preuve à divulgation nulle de connaissance, ces opérations se révèlent complexes et coûteuses, avec de nombreuses étapes. Nous avons donc dû contourner cette limitation pour que notre système fonctionne. Afin de transformer l'algorithme ECDSA en schéma avec lequel nous pouvons travailler, notre prouveur envoie R à la place et met en gage une valeur \(z\) calculée à partir de \(r\) et \(s\). L'équation de vérification s'en trouve ainsi simplifiée. Toute signature ECDSA peut être transformée en signature compatible avec notre schéma modifié (et vice versa), sans jamais faire appel à des connaissances secrètes. Le schéma se révèle donc tout aussi sûr que l'algorithme ECDSA.
Comme l'énoncé que nous souhaitons prouver comporte deux parties « Le message a été signé par une clé » et « La clé figure sur la liste », rien de plus naturel que de décomposer le problème représenté par la mise à l'épreuve de cet énoncé en deux parties. Le prouveur montre tout d'abord que la clé mise en gage a bien signé le message, avant de révéler que cette clé figure sur une liste. Le vérifieur procède également à la vérification de ces deux parties et, si les deux parties s'accordent, désigne la preuve comme valide.
Afin de prouver que la signature se vérifie sous une clé, nous avons dû utiliser une preuve montrant qu'un point de courbe elliptique constituait une puissance connue d'un autre point. Cette preuve représente en soi une preuve à divulgation nulle de connaissance assez simple, mais certaines étapes nécessitent elles-mêmes l'emploi de protocoles à apport de connaissance nul pour prouver que les points ont bien été ajoutés et le calcul effectué correctement. Elle consomme ainsi la majeure partie du temps de génération et de vérification des preuves. Une fois la preuve vérifiée, le vérifieur sait que son message a été signé par la clé publique mise en gage.
À l'étape suivante, le prouveur doit chercher où la clé se situe dans la liste, puis apporter la preuve que la clé figure bien dans cette dernière. Pour ce faire, nous utilisons la preuve à divulgation nulle de connaissance mise au point par Groth et Kohlweiss. Cette preuve s'engage d'abord sur l'expansion binaire du lieu de mise en gage dans la liste. Le prouveur doit ensuite prouver que cette expansion binaire est bien constituée de bits et fournir des informations complémentaires concernant sa méthode de démonstration. Grâce à ces informations et aux preuves, les deux parties peuvent calculer des polynômes valant zéro si la mise en gage concerne une valeur figurant sur la liste. Ce code se révèle étonnamment court pour une tâche aussi complexe.

Le vérifieur contrôle ensuite la preuve Groth-Kohlweiss indiquant que la clé mise en gage figure sur la liste, puis vérifie que le message signé est bien celui attendu. Il s'agit d'une preuve très efficace, même en cas d'augmentation de la taille de la liste, car le travail effectué par élément de la liste revient à une multiplication. Si tout correspond, nous savons alors que la signature a été générée par une clé de sécurité suffisamment sûre, sans obtenir aucune autre information. Si la vérification ne correspond pas, nous savons que quelque chose ne va pas.
Mise au point d'une courbe plus efficace
Nous avons transformé les énoncés sur les signatures ECDSA en énoncés sur les points de la courbe elliptique P-256, puis en énoncés sur l'arithmétique au sein du corps dans lequel la courbe P-256 est définie. Comme ces énoncés s'avèrent plus faciles à prouver à l'aide d'un groupe à la taille correspondant à celle du corps, nous avons dû en trouver un. Il s'agissait là d'un défi intéressant, car ce mode d'opération est à l'inverse de la manière dont nous faisons normalement les choses en cryptographie. Poursuivez la lecture si vous souhaitez voir comment nous avons résolu le problème. Sinon, passez à la section suivante.
Dans le domaine du chiffrement à courbe elliptique, nous commençons la plupart du temps par un corps de base pratique et recherchons des courbes elliptiques d'ordre premier ou presque premier comportant les propriétés adéquates pour notre application. Nous pouvons ainsi choisir des nombres premiers dotés de propriétés convenant aux équipements informatiques physiques. Lorsqu'il s'agit d'obtenir des courbes bien adaptées au couplage, nous recherchons généralement des courbes aux paramètres donnés par des polynômes connus.
Toutefois, comme nous souhaitions obtenir ici une courbe accompagnée d'un nombre donné de points, nous avons dû faire appel à des mécanismes assez avancés de la théorie des nombres pour la déterminer. C'est précisément cet aspect de nos recherches qui a rendu notre attestation à divulgation nulle aussi efficace qu'elle l'est actuellement.
Courbes elliptiques et plan complexe
Les courbes elliptiques sur le corps des nombres complexes sont particulièrement belles. Une courbe elliptique est isomorphe à un tore. Toutes les courbes complexes sont isomorphes aux tores sur le corps des nombres complexes, mais certaines comportent plusieurs trous.
On distingue les différentes courbes elliptiques selon leur épaisseur ou leur finesse dans les deux directions autour du tore. En imaginant une section transversale autour des trous du tore, nous voyons que nous pouvons obtenir un tore en prenant un rectangle et en collant les côtés. N'hésitez pas à consulter cette vidéo explicative montrant comment coller un tore.
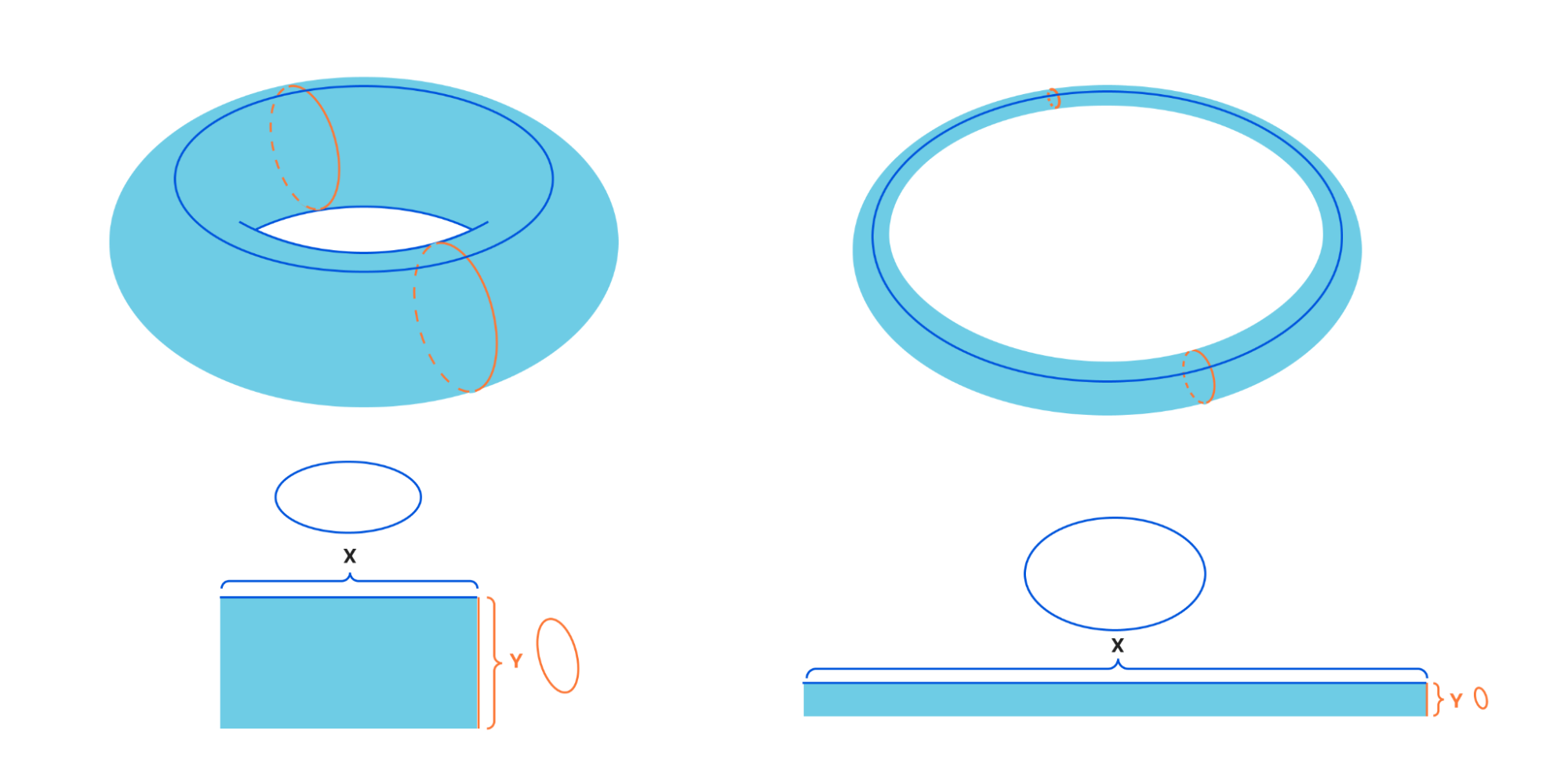
Au lieu de prendre un rectangle et de le coller, nous pouvons également imaginer prendre l'ensemble du plan, avant de le plier de manière à ce que chaque rectangle s'aligne. Ce faisant, les coins de ces rectangles s'alignent tous sur l'origine. Les coins forment alors ce que nous appelons un réseau et nous conservons toujours la possibilité de modifier l'échelle et d'effectuer une rotation afin que l'un des générateurs du réseau soit 1.
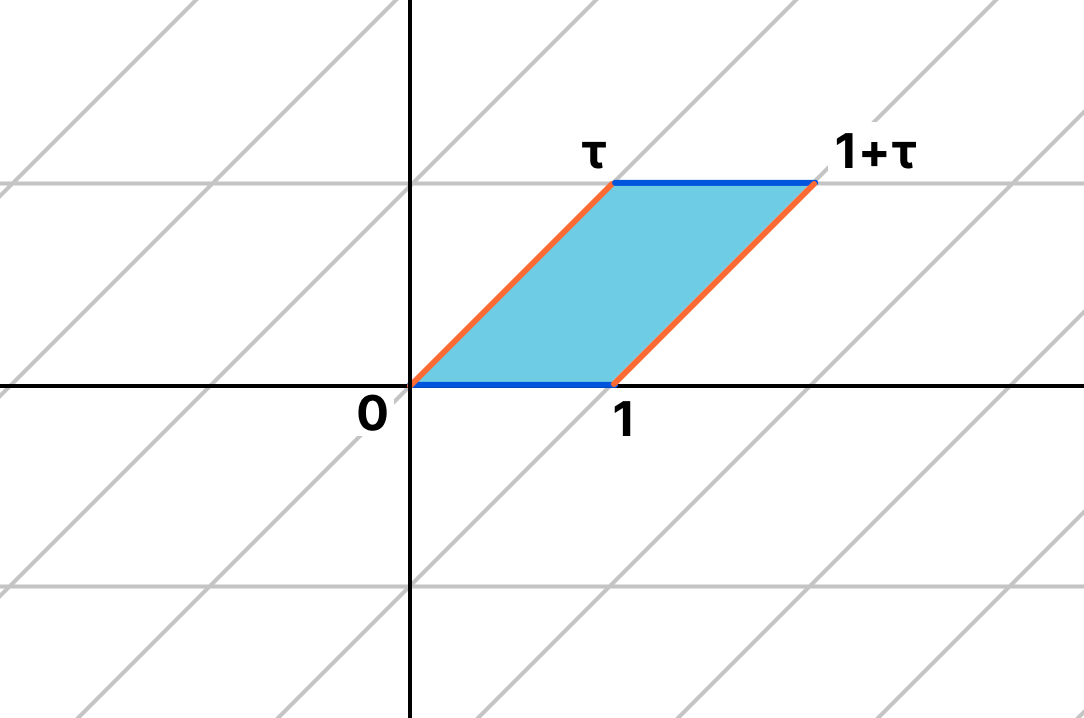
Vue sous cet angle, l'addition de nombres complexes devient une addition sur le tore, tout comme l'addition des entiers modulo 2 désigne une addition d'entiers, suivie d'une réduction modulo 2. Toutefois, avec les courbes elliptiques, nous sommes habitués à disposer d'équations algébriques pour l'addition et la multiplication, ainsi que pour les courbes elles-mêmes. Mais comment cette image analytique interagit-elle avec l'image algébrique ?
Après de nombreuses transformations géométriques classiques de formes complexes, nous constatons qu'un lien fort existe entre les deux. L'anneau des fonctions à valeurs complexes sur le réseau est ainsi généré par la fonction \(\mathcal{P}\) de Weierstrass et sa dérivée. Ces dernières permettent de répondre à l'équation algébrique ayant pour forme \(y^2 = x^3+ax+b\) tandis que les paramètres \(a\) et \(b\) constituent des fonctions du paramètre du réseau. Les formules classiques régissant l'addition algébrique de points sur des courbes elliptiques émergent de ce constat.
L'un des paramètres est le \(j\)-invariant, c'est-à-dire un invariant plus significatif sur le plan arithmétique que \(\tau\). Le \(j\)-invariant constitue une fonction de la courbe elliptique : les valeurs de \(\tau\) qui donnent lieu au même réseau produisent le même \(j\)-invariant, alors qu'elles peuvent être différentes pour \(a\) et \(b\). Il existe de nombreuses expressions pour \(j\), notamment la suivante :
https://dlmf.nist.gov/23.15#E7
Multiplication complexe et corps de classe
Prenons le réseau \(\{1, i\}\). Si nous multiplions ce réseau par \(i\), nous obtenons \(\{i, -1\}\), qui génère le même ensemble de points. Il s'agit d'un cas exceptionnel qui ne peut se produire que lorsque le nombre multiplicateur répond à une équation du second degré. Les éléments du réseau se révèlent alors étroitement liés aux solutions de cette dernière.
Un discriminant se trouve relié à ce type de réseau : le discriminant du corps quadratique associé à l'exemple. Dans notre exemple avec \(i\), ce discriminant est \(-4\), c'est-à-dire le discriminant de l'équation de second degré \(x^2 + 1\). Si par exemple nous devions plutôt prendre \(\sqrt{-5}\) et envisager le réseau \(\{1, \sqrt{-5}\}\), le discriminant serait \(-20\), soit le discriminant de l'équation \(x^2– 5\). Notez que différentes définitions du discriminant existent, modifiant le signe et ajoutant diverses puissances de \(2\).
On nomme endomorphismes les applications des courbes elliptiques vers elles-mêmes. La plupart de ces courbes n'ont comme endomorphismes que la multiplication par des entiers, mais certaines présentent des endomorphismes supplémentaires. Ainsi, la transformation du réseau \(\{1, i\}\) en courbe elliptique permet d'obtenir \( y^2 = x^3 + x \). Cette courbe dispose à présent d'un endomorphisme supplémentaire : si j'envoie \(y\) vers \(iy\) et \(x\) vers \(-x\), j'obtiens un point répondant à l'équation de courbe exprimée sous la forme \( (-iy) ^3 = (-x) ^ 2– x \). La répétition de cette application à deux reprises produit le même effet que l'inversion d'un point. Ce n'est donc pas une coïncidence si le fait de multiplier deux fois par i envoie un nombre complexe \(z\) vers \(-z\). Cet endomorphisme supplémentaire et la multiplication par i répondent donc à la même équation. On nomme multiplication complexe le fait de disposer d'un endomorphisme supplémentaire, en raison de la présence d'une multiplication par un nombre complexe. Lorsque le réseau dont provient une courbe elliptique présente une multiplication complexe, la courbe elliptique présente également une multiplication complexe et vice versa.
Tout ensemble d'objets mathématiques s'accompagne de questions et les courbes elliptiques à multiplication complexe ne font pas exception. Nous pouvons ainsi nous demander combien de courbes elliptiques existent pour un discriminant donné. Comment ce nombre augmente-t-il à mesure que le discriminant augmente lui aussi ? Certaines de ces questions n'ont d'ailleurs toujours pas de réponse aujourd'hui, malgré des années de recherche et d'expérimentation informatique. L'aspect essentiel pour les aborder repose sur le lien entre le réseau et l'arithmétique.
Au XIXe siècle, Gauss a étudié les formes quadratiques binaires, c'est-à-dire les équations de type \(ax ^2 + bxy + cy ^2\). Ces formes sont dites équivalentes s'il existe une substitution à coefficients entiers pour x et y qui transforme l'une en l'autre. Il s'agit là d'une notion fondamentale. En plus des algorithmes de réduction des formes quadratiques binaires, Gauss a également démontré qu'une loi de composition réunissait les formes quadratiques binaires d'un discriminant donné au sein d'un même groupe.
Par la suite, de nombreux théoriciens ont travaillé à créer un groupe idéal, associant les formes quadratiques à l'échec de la factorisation unique. Les formes \(x ^ 2 + 5y ^ 2\) et \(2x ^2 + 2xy + 3y ^2\) constituent ainsi deux formes quadratiques de discriminant \(-20\), liées à l'échec de la factorisation unique dans \(\mathbb{Z}[\sqrt{-5}]\).
Lorsque nous considérons les formes quadratiques binaires (les longueurs de vecteurs dans un plan, par exemple), chaque réseau donne une forme quadratique binaire jusqu'à l'équivalence. Les courbes elliptiques à multiplication complexe par un discriminant donné correspondent donc aux classes de formes quadratiques binaires associées à un discriminant donné, en lien avec l'arithmétique dans le corps quadratique. Trois questions en apparence très différentes reçoivent donc toutes la même réponse.
Qu'est-ce qui rend la multiplication complexe si importante dans la recherche de courbes ?
Lorsque nous prenons une courbe elliptique à coefficients intégraux et la considérons comme un nombre premier, cette dernière bénéficie d'un endomorphisme supplémentaire : l'endomorphisme de Frobénius qui envoie \(x\) vers \(x ^ p\) et \(y\) vers \(y ^p\) Cet endomorphisme répond à une équation quadratique et le terme linéaire de cette dernière correspond au nombre de points moins \(p+1\).
Si la courbe elliptique présente une multiplication complexe, il existe un autre endomorphisme, c'est-à-dire celui résultant de la multiplication complexe. Une courbe elliptique ne peut toutefois disposer que d'un seul endomorphisme supplémentaire, sauf s'il s'agit d'une supersingulière. Les courbes supersingulières sont très rares. L'endomorphisme de Frobénius et l'endomorphisme issu d'une multiplication complexe doivent donc être identiques. Comme nous avons commencé par la multiplication complexe, nous connaissons l'équation de second degré à laquelle le Frobenius doit répondre et donc le nombre de points.
Notre saga se conclut ainsi : pour trouver une courbe elliptique avec un ordre donné, cherchez des solutions à nombre entier à l'équation \(t ^ 2 + Dy ^2 = 4N\) pour petit \(D\) et laissez \(p = N - t + 1\), puis observez s'il s'agit d'un nombre premier. Factorisez ensuite le polynôme à corps de classe de Hilbert de \(D\) sur \(p\) et prenez l'une des racines modulo \(p\) comme invariant de notre courbe elliptique. Nous devrons peut-être effectuer une torsion quadratique pour obtenir le bon nombre de points, puisque \(t\) n'est identifié que jusqu'au signe.
Nous avons ainsi obtenu la courbe dont nous avions besoin pour prouver efficacement les relations sur le corps de base de P-256. L'ensemble de ces opérations mathématiques produisent un script qui s'exécute en quelques minutes et produit la courbe avec l'ordre souhaité.
Résultat de nos travaux
Après tous ces efforts (sans oublier un gros travail d'ingénierie supplémentaire pour rendre la preuve plus rapide grâce à l'optimisation des éléments qui la composent), nous sommes en mesure de générer une preuve en quelques secondes et de la vérifier en quelques centaines de millisecondes. Suffisamment rapide pour pouvoir être utilisé dans la pratique, ce résultat implique donc que les sites web qui souhaitent vérifier la sûreté des clés de sécurité peuvent le faire sans nuire à la confidentialité.
La seule information apprise par un site web appliquant notre technique consiste à savoir si la signature a été générée ou non par un jeton dont la clé d'attestation figure dans la liste qu'il a fournie. Contrairement à ce qui se produit lors de l'utilisation directe du processus WebAuthn, les sites ne recueillent pas d'informations plus détaillées, même si le fabricant a accidentellement créé un lot trop petit. Ainsi, plutôt que de protéger la confidentialité des utilisateurs à l'aide d'une approche reposant sur des politiques, nous avons supprimé les informations superflues.
Prochaines étapes : un effort collectif !
Notre démonstration atteste que nous disposons bien d'une mesure fonctionnelle de renforcement de la vie privée, fondée sur les preuves à divulgation nulle de connaissance. Nous continuons à l'améliorer, en lui ajoutant des fonctionnalités d'amélioration des performances et de la sécurité. Toutefois, notre travail ne s'arrêtera pas tant que nous n'aurons pas obtenu une extension WebAuthn capable de préserver la confidentialité et compatible avec l'ensemble des navigateurs, c'est-à-dire une fonction permettant de garantir aux utilisateurs que leurs données ne quitteront pas leur navigateur.
Nous ne disposons à l'heure actuelle que d'une démonstration de ce qui est possible : l'utilisation de preuves sans connaissance pour transformer le processus d'attestation WebAuthn en un système qui, de par sa conception même, traite chaque fabricant de manière égale, protège la confidentialité des utilisateurs et peut être utilisé par chaque site web. Les défis liés à la confidentialité des utilisateurs et résultant de l'utilisation à grande échelle du processus d'attestation peuvent recevoir une réponse.
Un système fiable et de grande qualité ne se limite pas aux connaissances cryptographiques de base. Afin d'éviter à l'expérience utilisateur d'être émaillée de messages d'avertissement concernant les informations écartées par notre processus de preuve à divulgation nulle de connaissance, nous devons renforcer l'intégration avec le navigateur. Nous avons également besoin d'un moyen sûr permettant aux utilisateurs d'appareils qui ne figurent pas sur notre liste de nous envoyer leur clé et de prouver leur fiabilité, ainsi qu'un moyen d'empêcher toute utilisation abusive de la liste visant à identifier des clés particulières.
En outre, cette méthode de vérification s'avère plus lourde que les anciennes, de sorte que les serveurs qui la mettent en œuvre doivent intégrer des mesures de limitation du débit et d'autres protections contre l'utilisation abusive. Les SNARKS offriraient un énorme avantage ici, mais ils présentent un coût certain en termes de taille de code pour la démonstration. En fin de compte, l'intégration de ces améliorations au sein d'une partie essentielle de l'écosystème web nécessite de travailler avec les utilisateurs, les navigateurs et les autres participants afin de trouver une solution qui leur convienne. N'hésitez pas à nous faire part de vos commentaires à l'adresse [email protected] si vous souhaitez contribuer au processus.
Notre attestation cryptographique de personnalité offre aux utilisateurs un moyen plus facile de démontrer leur nature d'être humain, mais aussi plus protecteur de la vie privée, que de nombreux autres fournisseurs ou solutions de remplacement aux CAPTCHA. Peu satisfaits des technologies les plus récentes en la matière, nous avons vu ici une occasion d'appliquer des techniques de chiffrement avancées pour améliorer la confidentialité de nos utilisateurs. Notre travail démontre donc que l'utilisation de preuves à divulgation nulle de connaissance peut renforcer les mesures de protection de la confidentialité proposées par les protocoles du monde réel.

