As engineers at Cloudflare quickly adapt our software stack to run on ARM, a few parts of our software stack have not been performing as well on ARM processors as they currently do on our Xeon® Silver 4116 CPUs. For the most part this is a matter of Intel specific optimizations some of which utilize SIMD or other special instructions.
One such example is the venerable jpegtran, one of the workhorses behind our Polish image optimization service.
A while ago I optimized our version of jpegtran for Intel processors. So when I ran a comparison on my test image, I was expecting that the Xeon would outperform ARM:
vlad@xeon:~$ time ./jpegtran -outfile /dev/null -progressive -optimise -copy none test.jpg
real 0m2.305s
user 0m2.059s
sys 0m0.252svlad@arm:~$ time ./jpegtran -outfile /dev/null -progressive -optimise -copy none test.jpg
real 0m8.654s
user 0m8.433s
sys 0m0.225sIdeally we want to have the ARM performing at or above 50% of the Xeon performance per core. This would make sure we have no performance regressions, and net performance gain, since the ARM CPUs have double the core count as our current 2 socket setup.
In this case, however, I was disappointed to discover an almost 4X slowdown.
Not one to despair, I figured out that applying the same optimizations I did for Intel would be trivial. Surely the NEON instructions map neatly to the SSE instructions I used before?

CC BY-SA 2.0 image by viZZZual.com
What is NEON
NEON is the ARMv8 version of SIMD, Single Instruction Multiple Data instruction set, where a single operation performs (generally) the same operation on several operands.
NEON operates on 32 dedicated 128-bit registers, similarly to Intel SSE. It can perform operations on 32-bit and 64-bit floating point numbers, or 8-bit, 16-bit, 32-bit and 64-bit signed or unsigned integers.
As with SSE you can program either in the assembly language, or in C using intrinsics. The intrinsics are usually easier to use, and depending on the application and the compiler can provide better performance, however intrinsics based code tends to be quite verbose.
If you opt to use the NEON intrinsics you have to include <arm_neon.h>. While SSE intrinsic use __m128i for all SIMD integer operations, the intrinsics for NEON have distinct type for each integer and float width. For example operations on signed 16-bit integers use the int16x8_t type, which we are going to use. Similarly there is a uint16x8_t type for unsigned integer, as well as int8x16_t, int32x4_t and int64x2_t and their uint derivatives, that are self explanatory.
Getting started
Running perf tells me that the same two culprits are responsible for most of the CPU time spent:
perf record ./jpegtran -outfile /dev/null -progressive -optimise -copy none test.jpeg
perf report
71.24% lt-jpegtran libjpeg.so.9.1.0 [.] encode_mcu_AC_refine
15.24% lt-jpegtran libjpeg.so.9.1.0 [.] encode_mcu_AC_firstAha, encode_mcu_AC_refine and encode_mcu_AC_first, my old nemeses!
The straightforward approach
encode_mcu_AC_refine
Let's recoup the optimizations we applied to encode_mcu_AC_refine previously. The function has two loops, with the heavier loop performing the following operation:
for (k = cinfo->Ss; k <= Se; k++) {
temp = (*block)[natural_order[k]];
if (temp < 0)
temp = -temp; /* temp is abs value of input */
temp >>= Al; /* apply the point transform */
absvalues[k] = temp; /* save abs value for main pass */
if (temp == 1)
EOB = k; /* EOB = index of last newly-nonzero coef */
}And the SSE solution to this problem was:
__m128i x1 = _mm_setzero_si128(); // Load 8 16-bit values sequentially
x1 = _mm_insert_epi16(x1, (*block)[natural_order[k+0]], 0);
x1 = _mm_insert_epi16(x1, (*block)[natural_order[k+1]], 1);
x1 = _mm_insert_epi16(x1, (*block)[natural_order[k+2]], 2);
x1 = _mm_insert_epi16(x1, (*block)[natural_order[k+3]], 3);
x1 = _mm_insert_epi16(x1, (*block)[natural_order[k+4]], 4);
x1 = _mm_insert_epi16(x1, (*block)[natural_order[k+5]], 5);
x1 = _mm_insert_epi16(x1, (*block)[natural_order[k+6]], 6);
x1 = _mm_insert_epi16(x1, (*block)[natural_order[k+7]], 7);
x1 = _mm_abs_epi16(x1); // Get absolute value of 16-bit integers
x1 = _mm_srli_epi16(x1, Al); // >> 16-bit integers by Al bits
_mm_storeu_si128((__m128i*)&absvalues[k], x1); // Store
x1 = _mm_cmpeq_epi16(x1, _mm_set1_epi16(1)); // Compare to 1
unsigned int idx = _mm_movemask_epi8(x1); // Extract byte mask
EOB = idx? k + 16 - __builtin_clz(idx)/2 : EOB; // Compute indexFor the most part the transition to NEON is indeed straightforward.
To initialize a register to all zeros, we can use the vdupq_n_s16 intrinsic, that duplicates a given value across all lanes of a register. The insertions are performed with the vsetq_lane_s16 intrinsic. Use vabsq_s16 to get the absolute values.
The shift right instruction made me pause for a while. I simply couldn't find an instruction that can shift right by a non constant integer value. It doesn't exist. However the solution is very simple, you shift left by a negative amount! The intrinsic for that is vshlq_s16.
The absence of a right shift instruction is no coincidence. Unlike the x86 instruction set, that can theoretically support arbitrarily long instructions, and thus don't have to think twice before adding a new instruction, no matter how specialized or redundant it is, ARMv8 instruction set can only support 32-bit long instructions, and have a very limited opcode space. For this reason the instruction set is much more concise, and many instructions are in fact aliases to other instruction. Even the most basic MOV instruction is an alias for ORR (binary or). That means that programming for ARM and NEON sometimes requires greater creativity.
The final step of the loop, is comparing each element to 1, then getting the mask. Comparing for equality is performed with vceqq_s16. But again there is no operation to extract the mask. That is a problem. However, instead of getting a bitmask, it is possible to extract a whole byte from every lane into a 64-bit value, by first applying vuzp1q_u8 to the comparison result. vuzp1q_u8 interleaves the even indexed bytes of two vectors (whereas vuzp2q_u8 interleaves the odd indexes). So the solution would look something like that:
int16x8_t zero = vdupq_n_s16(0);
int16x8_t al_neon = vdupq_n_s16(-Al);
int16x8_t x0 = zero;
int16x8_t x1 = zero;
// Load 8 16-bit values sequentially
x1 = vsetq_lane_s16((*block)[natural_order[k+0]], x1, 0);
// Interleave the loads to compensate for latency
x0 = vsetq_lane_s16((*block)[natural_order[k+1]], x0, 1);
x1 = vsetq_lane_s16((*block)[natural_order[k+2]], x1, 2);
x0 = vsetq_lane_s16((*block)[natural_order[k+3]], x0, 3);
x1 = vsetq_lane_s16((*block)[natural_order[k+4]], x1, 4);
x0 = vsetq_lane_s16((*block)[natural_order[k+5]], x0, 5);
x1 = vsetq_lane_s16((*block)[natural_order[k+6]], x1, 6);
x0 = vsetq_lane_s16((*block)[natural_order[k+7]], x0, 7);
int16x8_t x = vorrq_s16(x1, x0);
x = vabsq_s16(x); // Get absolute value of 16-bit integers
x = vshlq_s16(x, al_neon); // >> 16-bit integers by Al bits
vst1q_s16(&absvalues[k], x); // Store
uint8x16_t is_one = vreinterpretq_u8_u16(vceqq_s16(x, one)); // Compare to 1
is_one = vuzp1q_u8(is_one, is_one); // Compact the compare result into 64 bits
uint64_t idx = vgetq_lane_u64(vreinterpretq_u64_u8(is_one), 0); // Extract
EOB = idx ? k + 8 - __builtin_clzl(idx)/8 : EOB; // Get the indexNote the intrinsics for explicit type casts. They don't actually emit any instructions, since regardless of the type the operands always occupy the same registers.
On to the second loop:
if ((temp = absvalues[k]) == 0) {
r++;
continue;
}The SSE solution was:
__m128i t = _mm_loadu_si128((__m128i*)&absvalues[k]);
t = _mm_cmpeq_epi16(t, _mm_setzero_si128()); // Compare to 0
int idx = _mm_movemask_epi8(t); // Extract byte mask
if (idx == 0xffff) { // Skip all zeros
r += 8;
k += 8;
continue;
} else { // Skip up to the first nonzero
int skip = __builtin_ctz(~idx)/2;
r += skip;
k += skip;
if (k>Se) break; // Stop if gone too far
}
temp = absvalues[k]; // Load the next nonzero valueBut we already know that there is no way to extract the byte mask. Instead of using NEON I chose to simply skip four zero values at a time, using 64-bit integers, like so:
uint64_t tt, *t = (uint64_t*)&absvalues[k];
if ( (tt = *t) == 0) while ( (tt = *++t) == 0); // Skip while all zeroes
int skip = __builtin_ctzl(tt)/16 + ((int64_t)t -
(int64_t)&absvalues[k])/2; // Get index of next nonzero
k += skip;
r += skip;
temp = absvalues[k];How fast are we now?
vlad@arm:~$ time ./jpegtran -outfile /dev/null -progressive -optimise -copy none test.jpg
real 0m4.008s
user 0m3.770s
sys 0m0.241sWow, that is incredible. Over 2X speedup!
encode_mcu_AC_first
The other function is quite similar, but the logic slightly differs on the first pass:
temp = (*block)[natural_order[k]];
if (temp < 0) {
temp = -temp; // Temp is abs value of input
temp >>= Al; // Apply the point transform
temp2 = ~temp;
} else {
temp >>= Al; // Apply the point transform
temp2 = temp;
}
t1[k] = temp;
t2[k] = temp2;Here it is required to assign the absolute value of temp to t1[k], and its inverse to t2[k] if temp is negative, otherwise t2[k] assigned the same value as t1[k].
To get the inverse of a value, we use the vmvnq_s16 intrinsic, to check if the values are negative we need to compare with zero using the vcgezq_s16 and finally selecting based on the mask using vbslq_s16.
int16x8_t zero = vdupq_n_s16(0);
int16x8_t al_neon = vdupq_n_s16(-Al);
int16x8_t x0 = zero;
int16x8_t x1 = zero;
// Load 8 16-bit values sequentially
x1 = vsetq_lane_s16((*block)[natural_order[k+0]], x1, 0);
// Interleave the loads to compensate for latency
x0 = vsetq_lane_s16((*block)[natural_order[k+1]], x0, 1);
x1 = vsetq_lane_s16((*block)[natural_order[k+2]], x1, 2);
x0 = vsetq_lane_s16((*block)[natural_order[k+3]], x0, 3);
x1 = vsetq_lane_s16((*block)[natural_order[k+4]], x1, 4);
x0 = vsetq_lane_s16((*block)[natural_order[k+5]], x0, 5);
x1 = vsetq_lane_s16((*block)[natural_order[k+6]], x1, 6);
x0 = vsetq_lane_s16((*block)[natural_order[k+7]], x0, 7);
int16x8_t x = vorrq_s16(x1, x0);
uint16x8_t is_positive = vcgezq_s16(x); // Get positive mask
x = vabsq_s16(x); // Get absolute value of 16-bit integers
x = vshlq_s16(x, al_neon); // >> 16-bit integers by Al bits
int16x8_t n = vmvnq_s16(x); // Binary inverse
n = vbslq_s16(is_positive, x, n); // Select based on positive mask
vst1q_s16(&t1[k], x); // Store
vst1q_s16(&t2[k], n);And the moment of truth:
vlad@arm:~$ time ./jpegtran -outfile /dev/null -progressive -optimise -copy none test.jpg
real 0m3.480s
user 0m3.243s
sys 0m0.241sOverall 2.5X speedup from the original C implementation, but still 1.5X slower than Xeon.
Batch benchmark
While the improvement for the single image was impressive, it is not necessarily representative of all jpeg files. To understand the impact on overall performance I ran jpegtran over a set of 34,159 actual images from one of our caches. The total size of those images was 3,325,253KB. The total size after jpegtran was 3,067,753KB, or 8% improvement on average.
Using one thread, the Intel Xeon managed to process all those images in 14 minutes and 43 seconds. The original jpegtran on our ARM server took 29 minutes and 34 seconds. The improved jpegtran took only 13 minutes and 52 seconds, slightly outperforming even the Xeon processor, despite losing on the test image.

Going deeper
3.48 seconds, down from 8.654 represents a respectful 2.5X speedup.
It definitely meets the goal of being at least 50% as fast as Xeon, and it is faster in the batch benchmark, but it still feels like it is slower than it could be.
While going over the ARMv8 NEON instruction set, I found several unique instructions, that have no equivalent in SSE.
The first such instruction is TBL. It works as a lookup table, that can lookup 8 or 16 bytes from one to four consecutive registers. In the single register variant it is similar to the pshufb SSE instruction. In the four register variant, however, it can simultaneously lookup 16 bytes in a 64 byte table! What sorcery is that?
The intrinsic to use the 4 register variant is vqtbl4q_u8. Interestingly there is an instruction that can lookup 64 bytes in AVX-512, but we don't want to use that.
The next interesting thing I found, are instructions that can load or store and de/interleave data at the same time. They can load or store up to four registers simultaneously, while de/interleaving two, three or even four elements, of any supported width. The specifics are well presented in here. The load intrinsics used are of the form: vldNq_uW, where N can be 1,2,3,4 to indicate the interleave factor and W can be 8, 16, 32 or 64. Similarly vldNq_sW is used for signed types.
Finally very interesting instructions are the shift left/right and insert SLI and SRI. What they do is they shift the elements left or right, like a regular shift would, however instead of shifting in zero bits, the zeros are replaced with the original bits of the destination register! An intrinsic for that would look like vsliq_n_u16 or vsriq_n_u32.
Applying the new instructions
It might not be visible at first how those new instruction can help. Since I didn't have much time to dig into libjpeg or the jpeg spec, I had to resolve to heuristics.
From a quick look it became apparent that *block is defined as an array of 64 16-bit values. natural_order is an array of 32-bit integers that varies in length depending on the real block size, but is always padded with 16 entries. Also, despite the fact that it uses integers, the values are indexes in the range [0..63].
Another interesting observation is that blocks of size 64 are the most common by far for both encode_mcu_AC_refine and encode_mcu_AC_first. And it always makes sense to optimize for the most common case.
So essentially what we have here, is a 64 entry lookup table *block that uses natural_order as indices. Hmm, 64 entry lookup table, where did I see that before? Of course, the TBL instruction. Although TBL looks up bytes, and we need to lookup shorts, it is easy to do, since NEON lets us load and deinterleave the short into bytes in a single instruction using LD2, then we can use two lookups for each byte individually, and finally interleave again with ZIP1 and ZIP2. Similarly despite the fact that the indices are integers, and we only need the least significant byte of each, we can use LD4 to deinterleave them into bytes (the kosher way of course would be to rewrite the library to use bytes, but I wanted to avoid big changes).
After the data loading step is done, the point transforms for both functions remain the same, but in the end, to get a single bitmask for all 64 values we can use SLI and SRI to intelligently align the bits such that only one bit of each comparison mask remains, using TBL again to combine them.
For whatever reason, the compiler in that case produces somewhat suboptimal code, so I had to revert to assembly language for this specific optimization.
The code for encode_mcu_AC_refine:
# Load and deintreleave the block
ld2 {v0.16b - v1.16b}, [x0], 32
ld2 {v16.16b - v17.16b}, [x0], 32
ld2 {v18.16b - v19.16b}, [x0], 32
ld2 {v20.16b - v21.16b}, [x0]
mov v4.16b, v1.16b
mov v5.16b, v17.16b
mov v6.16b, v19.16b
mov v7.16b, v21.16b
mov v1.16b, v16.16b
mov v2.16b, v18.16b
mov v3.16b, v20.16b
# Load the order
ld4 {v16.16b - v19.16b}, [x1], 64
ld4 {v17.16b - v20.16b}, [x1], 64
ld4 {v18.16b - v21.16b}, [x1], 64
ld4 {v19.16b - v22.16b}, [x1]
# Table lookup, LSB and MSB independently
tbl v20.16b, {v0.16b - v3.16b}, v16.16b
tbl v16.16b, {v4.16b - v7.16b}, v16.16b
tbl v21.16b, {v0.16b - v3.16b}, v17.16b
tbl v17.16b, {v4.16b - v7.16b}, v17.16b
tbl v22.16b, {v0.16b - v3.16b}, v18.16b
tbl v18.16b, {v4.16b - v7.16b}, v18.16b
tbl v23.16b, {v0.16b - v3.16b}, v19.16b
tbl v19.16b, {v4.16b - v7.16b}, v19.16b
# Interleave MSB and LSB back
zip1 v0.16b, v20.16b, v16.16b
zip2 v1.16b, v20.16b, v16.16b
zip1 v2.16b, v21.16b, v17.16b
zip2 v3.16b, v21.16b, v17.16b
zip1 v4.16b, v22.16b, v18.16b
zip2 v5.16b, v22.16b, v18.16b
zip1 v6.16b, v23.16b, v19.16b
zip2 v7.16b, v23.16b, v19.16b
# -Al
neg w3, w3
dup v16.8h, w3
# Absolute then shift by Al
abs v0.8h, v0.8h
sshl v0.8h, v0.8h, v16.8h
abs v1.8h, v1.8h
sshl v1.8h, v1.8h, v16.8h
abs v2.8h, v2.8h
sshl v2.8h, v2.8h, v16.8h
abs v3.8h, v3.8h
sshl v3.8h, v3.8h, v16.8h
abs v4.8h, v4.8h
sshl v4.8h, v4.8h, v16.8h
abs v5.8h, v5.8h
sshl v5.8h, v5.8h, v16.8h
abs v6.8h, v6.8h
sshl v6.8h, v6.8h, v16.8h
abs v7.8h, v7.8h
sshl v7.8h, v7.8h, v16.8h
# Store
st1 {v0.16b - v3.16b}, [x2], 64
st1 {v4.16b - v7.16b}, [x2]
# Constant 1
movi v16.8h, 0x1
# Compare with 0 for zero mask
cmeq v17.8h, v0.8h, #0
cmeq v18.8h, v1.8h, #0
cmeq v19.8h, v2.8h, #0
cmeq v20.8h, v3.8h, #0
cmeq v21.8h, v4.8h, #0
cmeq v22.8h, v5.8h, #0
cmeq v23.8h, v6.8h, #0
cmeq v24.8h, v7.8h, #0
# Compare with 1 for EOB mask
cmeq v0.8h, v0.8h, v16.8h
cmeq v1.8h, v1.8h, v16.8h
cmeq v2.8h, v2.8h, v16.8h
cmeq v3.8h, v3.8h, v16.8h
cmeq v4.8h, v4.8h, v16.8h
cmeq v5.8h, v5.8h, v16.8h
cmeq v6.8h, v6.8h, v16.8h
cmeq v7.8h, v7.8h, v16.8h
# For both masks -> keep only one byte for each comparison
uzp1 v0.16b, v0.16b, v1.16b
uzp1 v1.16b, v2.16b, v3.16b
uzp1 v2.16b, v4.16b, v5.16b
uzp1 v3.16b, v6.16b, v7.16b
uzp1 v17.16b, v17.16b, v18.16b
uzp1 v18.16b, v19.16b, v20.16b
uzp1 v19.16b, v21.16b, v22.16b
uzp1 v20.16b, v23.16b, v24.16b
# Shift left and insert (int16) to get a single bit from even to odd bytes
sli v0.8h, v0.8h, 15
sli v1.8h, v1.8h, 15
sli v2.8h, v2.8h, 15
sli v3.8h, v3.8h, 15
sli v17.8h, v17.8h, 15
sli v18.8h, v18.8h, 15
sli v19.8h, v19.8h, 15
sli v20.8h, v20.8h, 15
# Shift right and insert (int32) to get two bits from off to even indices
sri v0.4s, v0.4s, 18
sri v1.4s, v1.4s, 18
sri v2.4s, v2.4s, 18
sri v3.4s, v3.4s, 18
sri v17.4s, v17.4s, 18
sri v18.4s, v18.4s, 18
sri v19.4s, v19.4s, 18
sri v20.4s, v20.4s, 18
# Regular shift right to align the 4 bits at the bottom of each int64
ushr v0.2d, v0.2d, 12
ushr v1.2d, v1.2d, 12
ushr v2.2d, v2.2d, 12
ushr v3.2d, v3.2d, 12
ushr v17.2d, v17.2d, 12
ushr v18.2d, v18.2d, 12
ushr v19.2d, v19.2d, 12
ushr v20.2d, v20.2d, 12
# Shift left and insert (int64) to combine all 8 bits into one byte
sli v0.2d, v0.2d, 36
sli v1.2d, v1.2d, 36
sli v2.2d, v2.2d, 36
sli v3.2d, v3.2d, 36
sli v17.2d, v17.2d, 36
sli v18.2d, v18.2d, 36
sli v19.2d, v19.2d, 36
sli v20.2d, v20.2d, 36
# Combine all the byte mask insto a bit 64-bit mask for EOB and zero masks
ldr d4, .shuf_mask
tbl v5.8b, {v0.16b - v3.16b}, v4.8b
tbl v6.8b, {v17.16b - v20.16b}, v4.8b
# Extract lanes
mov x0, v5.d[0]
mov x1, v6.d[0]
# Compute EOB
rbit x0, x0
clz x0, x0
mov x2, 64
sub x0, x2, x0
# Not of zero mask (so 1 bits indecates non-zeroes)
mvn x1, x1
retIf you look carefully at the code, you will see, that I decided that while generating the mask to find EOB is useful, I can use the same method to generate the mask for zero values, and then I can find the next nonzero value, and zero runlength this way:
uint64_t skip =__builtin_clzl(zero_mask << k);
r += skip;
k += skip;Similarly for encode_mcu_AC_first:
# Load the block
ld2 {v0.16b - v1.16b}, [x0], 32
ld2 {v16.16b - v17.16b}, [x0], 32
ld2 {v18.16b - v19.16b}, [x0], 32
ld2 {v20.16b - v21.16b}, [x0]
mov v4.16b, v1.16b
mov v5.16b, v17.16b
mov v6.16b, v19.16b
mov v7.16b, v21.16b
mov v1.16b, v16.16b
mov v2.16b, v18.16b
mov v3.16b, v20.16b
# Load the order
ld4 {v16.16b - v19.16b}, [x1], 64
ld4 {v17.16b - v20.16b}, [x1], 64
ld4 {v18.16b - v21.16b}, [x1], 64
ld4 {v19.16b - v22.16b}, [x1]
# Table lookup, LSB and MSB independently
tbl v20.16b, {v0.16b - v3.16b}, v16.16b
tbl v16.16b, {v4.16b - v7.16b}, v16.16b
tbl v21.16b, {v0.16b - v3.16b}, v17.16b
tbl v17.16b, {v4.16b - v7.16b}, v17.16b
tbl v22.16b, {v0.16b - v3.16b}, v18.16b
tbl v18.16b, {v4.16b - v7.16b}, v18.16b
tbl v23.16b, {v0.16b - v3.16b}, v19.16b
tbl v19.16b, {v4.16b - v7.16b}, v19.16b
# Interleave MSB and LSB back
zip1 v0.16b, v20.16b, v16.16b
zip2 v1.16b, v20.16b, v16.16b
zip1 v2.16b, v21.16b, v17.16b
zip2 v3.16b, v21.16b, v17.16b
zip1 v4.16b, v22.16b, v18.16b
zip2 v5.16b, v22.16b, v18.16b
zip1 v6.16b, v23.16b, v19.16b
zip2 v7.16b, v23.16b, v19.16b
# -Al
neg w4, w4
dup v24.8h, w4
# Compare with 0 to get negative mask
cmge v16.8h, v0.8h, #0
# Absolute value and shift by Al
abs v0.8h, v0.8h
sshl v0.8h, v0.8h, v24.8h
cmge v17.8h, v1.8h, #0
abs v1.8h, v1.8h
sshl v1.8h, v1.8h, v24.8h
cmge v18.8h, v2.8h, #0
abs v2.8h, v2.8h
sshl v2.8h, v2.8h, v24.8h
cmge v19.8h, v3.8h, #0
abs v3.8h, v3.8h
sshl v3.8h, v3.8h, v24.8h
cmge v20.8h, v4.8h, #0
abs v4.8h, v4.8h
sshl v4.8h, v4.8h, v24.8h
cmge v21.8h, v5.8h, #0
abs v5.8h, v5.8h
sshl v5.8h, v5.8h, v24.8h
cmge v22.8h, v6.8h, #0
abs v6.8h, v6.8h
sshl v6.8h, v6.8h, v24.8h
cmge v23.8h, v7.8h, #0
abs v7.8h, v7.8h
sshl v7.8h, v7.8h, v24.8h
# ~
mvn v24.16b, v0.16b
mvn v25.16b, v1.16b
mvn v26.16b, v2.16b
mvn v27.16b, v3.16b
mvn v28.16b, v4.16b
mvn v29.16b, v5.16b
mvn v30.16b, v6.16b
mvn v31.16b, v7.16b
# Select
bsl v16.16b, v0.16b, v24.16b
bsl v17.16b, v1.16b, v25.16b
bsl v18.16b, v2.16b, v26.16b
bsl v19.16b, v3.16b, v27.16b
bsl v20.16b, v4.16b, v28.16b
bsl v21.16b, v5.16b, v29.16b
bsl v22.16b, v6.16b, v30.16b
bsl v23.16b, v7.16b, v31.16b
# Store t1
st1 {v0.16b - v3.16b}, [x2], 64
st1 {v4.16b - v7.16b}, [x2]
# Store t2
st1 {v16.16b - v19.16b}, [x3], 64
st1 {v20.16b - v23.16b}, [x3]
# Compute zero mask like before
cmeq v17.8h, v0.8h, #0
cmeq v18.8h, v1.8h, #0
cmeq v19.8h, v2.8h, #0
cmeq v20.8h, v3.8h, #0
cmeq v21.8h, v4.8h, #0
cmeq v22.8h, v5.8h, #0
cmeq v23.8h, v6.8h, #0
cmeq v24.8h, v7.8h, #0
uzp1 v17.16b, v17.16b, v18.16b
uzp1 v18.16b, v19.16b, v20.16b
uzp1 v19.16b, v21.16b, v22.16b
uzp1 v20.16b, v23.16b, v24.16b
sli v17.8h, v17.8h, 15
sli v18.8h, v18.8h, 15
sli v19.8h, v19.8h, 15
sli v20.8h, v20.8h, 15
sri v17.4s, v17.4s, 18
sri v18.4s, v18.4s, 18
sri v19.4s, v19.4s, 18
sri v20.4s, v20.4s, 18
ushr v17.2d, v17.2d, 12
ushr v18.2d, v18.2d, 12
ushr v19.2d, v19.2d, 12
ushr v20.2d, v20.2d, 12
sli v17.2d, v17.2d, 36
sli v18.2d, v18.2d, 36
sli v19.2d, v19.2d, 36
sli v20.2d, v20.2d, 36
ldr d4, .shuf_mask
tbl v6.8b, {v17.16b - v20.16b}, v4.8b
mov x0, v6.d[0]
mvn x0, x0
retFinal results and power
The final version of our jpegtran managed to reduce the test image in 2.756 seconds. Or an extra 1.26X speedup, that gets it incredibly close to the performance of the Xeon on that image. As a bonus batch performance also improved!
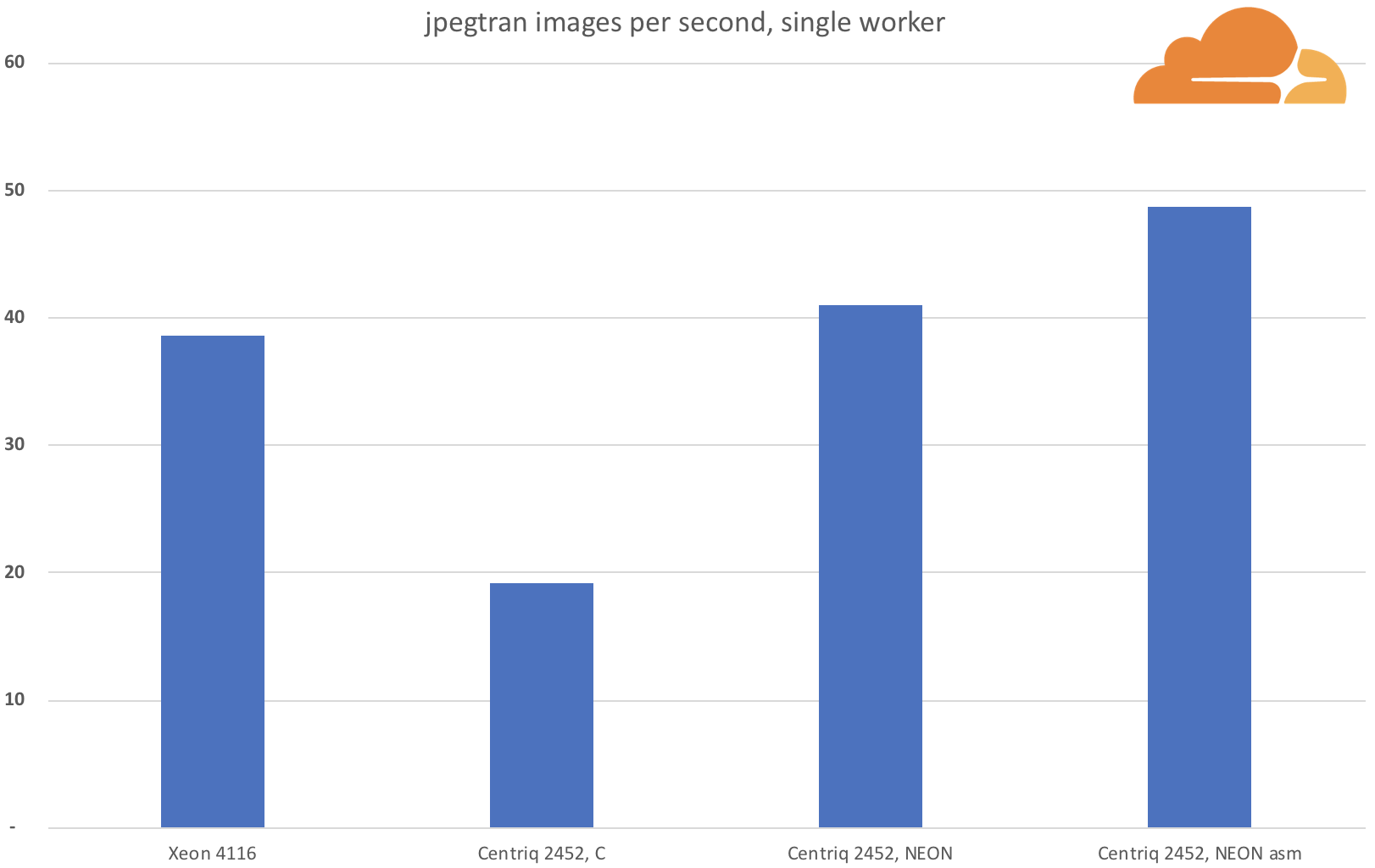
Another favorite part of mine, working with the Qualcomm Centriq CPU is the ability to take power readings, and be pleasantly surprised every time.

With the new implementation Centriq outperforms the Xeon at batch reduction for every number of workers. We usually run Polish with four workers, for which Centriq is now 1.3 times faster while also 6.5 times more power efficient.
Conclusion
It is evident that the Qualcomm Centriq is a powerful processor, that definitely provides a good bang for a buck. However, years of Intel leadership in the server and desktop space mean that a lot of software is better optimized for Intel processors.
For the most part writing optimizations for ARMv8 is not difficult, and we will be adjusting our software as needed, and publishing our efforts as we go.
You can find the updated code on our Github page.


